题目内容
若有一段演绎推理：“大前提：对任意实数a，都有（
）n=a．小前提：已知a=-2为实数．结论：（
）4=-2．”这个结论显然错误，是因为（ ）
| n | a |
| 4 | -2 |
| A、大前提错误 |
| B、小前提错误 |
| C、推理形式错误 |
| D、非以上错误 |
考点：演绎推理的基本方法
专题：证明题,推理和证明
分析：本题考查的知识点是演绎推理的基本方法，在使用三段论推理证明中，如果命题是错误的，则可能是“大前提”错误，也可能是“小前提”错误，也可能是逻辑错误．
解答：
解：对任意实数a，都有（
）n=a，a＜0，n为偶数时，显然不成立．
故大前提错误．
故选：A．
| n | a |
故大前提错误．
故选：A．
点评：本题是一个简单的演绎推理，这种问题不用进行运算，只要根据所学的知识点，判断这种说法是否正确，是一个基础题．
练习册系列答案
一线名师提优试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
某车间为了规定工时定额，需要确定加工零件所花费的时间，为此进行了5次试验．根据收集到的数据（如下表），由最小二乘法求得回归方程
=0.74x+50
则m+n的值为（ ）
 |
| y |
| 零件数x（个） | 10 | 20 | 30 | 40 | 50 |
| 加工时间y（min） | 62 | m | n | 81 | 89 |
| A、137 | B、129 |
| C、121 | D、118 |
在三角形ABC中，bcosC=CcosB，则三角形△ABC为（ ）
| A、等腰直角三角形 |
| B、等腰三角形 |
| C、等边三角形 |
| D、直角三角形 |
不等式|x+1|（2x-1）≥0的解集是（ ）
A、[
| ||
B、（-∞，-1]∪[
| ||
C、{-1}∪[
| ||
D、[-1，-
|
独立性检验中，假设H0：变量X与变量Y没有关系，则在H0成立的情况下，P（K2≥6.635）≈0.010表示的意义是（ ）
| A、在犯错误的概率不超过0.1%的前提下，认为“变量X与变量Y有关” |
| B、在犯错误的概率不超过0.1%的前提下，认为“变量X与变量Y无关” |
| C、有99%以上的把握认为“变量X与变量Y无关 |
| D、有99%以上的把握认为“变量X与变量Y有关” |
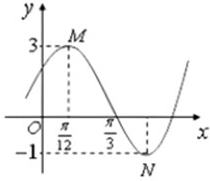
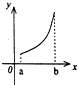
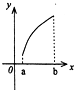
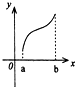
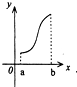
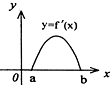设f′（x）是f（x）的导函数，f′（x）的图象如图所示，则f（x）的图象只可能是（ ）
