题目内容
在△ABC中,A=60°,b=1,c=4,则△ABC外接圆的直径为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、2
|
考点:余弦定理
专题:解三角形
分析:利用余弦定理列出关系式,将cosA,b,c的值代入求出a的值,利用正弦定理即可求出外接圆直径.
解答:
解:∵在△ABC中,A=60°,b=1,c=4,
∴由余弦定理得:a2=b2+c2-2bccosA=1+16-4=13,即a=
,
由正弦定理得:
=2R,即2R=
=
.
故选:B.
∴由余弦定理得:a2=b2+c2-2bccosA=1+16-4=13,即a=
| 13 |
由正弦定理得:
| a |
| sinA |
| ||||
|
2
| ||
| 3 |
故选:B.
点评:此题考查了正弦、余弦定理,以及特殊角的三角函数值,熟练掌握定理是解本题的关键.

练习册系列答案
相关题目
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了5次试验.根据收集到的数据(如下表),由最小二乘法求得回归方程
=0.74x+50
则m+n的值为( )
 |
| y |
| 零件数x(个) | 10 | 20 | 30 | 40 | 50 |
| 加工时间y(min) | 62 | m | n | 81 | 89 |
| A、137 | B、129 |
| C、121 | D、118 |
不等式|x+1|(2x-1)≥0的解集是( )
A、[
| ||
B、(-∞,-1]∪[
| ||
C、{-1}∪[
| ||
D、[-1,-
|
独立性检验中,假设H0:变量X与变量Y没有关系,则在H0成立的情况下,P(K2≥6.635)≈0.010表示的意义是( )
| A、在犯错误的概率不超过0.1%的前提下,认为“变量X与变量Y有关” |
| B、在犯错误的概率不超过0.1%的前提下,认为“变量X与变量Y无关” |
| C、有99%以上的把握认为“变量X与变量Y无关 |
| D、有99%以上的把握认为“变量X与变量Y有关” |
已知sin(π-α)=-
,π<α<
,则tanα=( )
| 12 |
| 13 |
| 3π |
| 2 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
给出下列三个函数的图象:
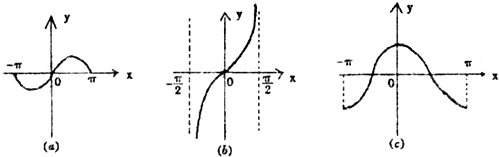
它们对应的函数表达式分别满足下列性质中的一条:
①f(2x)=2[f(x)]2-1
②f(x+y)=
③[f(2x)]2=4[f(x)]2(1-[f(x)]2)
则正确的对应方式是( )

它们对应的函数表达式分别满足下列性质中的一条:
①f(2x)=2[f(x)]2-1
②f(x+y)=
| f(x)+f(y) |
| 1-f(x)f(y) |
③[f(2x)]2=4[f(x)]2(1-[f(x)]2)
则正确的对应方式是( )
| A、(a)-①,(b)-②,(c)-③ |
| B、(b)-①,(c)-②,(a)-③ |
| C、(c)-①,(b)-②,(a)-③ |
| D、(a)-①,(c)-②,(b)-③ |
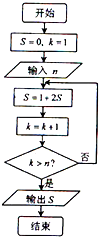 阅读如图所示的程序框图,运行相应的程序,如果输入某个正整数n后,输出的S∈(30,40),那么n的值为( )
阅读如图所示的程序框图,运行相应的程序,如果输入某个正整数n后,输出的S∈(30,40),那么n的值为( )