题目内容
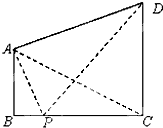 如图,两座建筑物AB,CD的底部都在同一个水平面上,且均与水平面垂直,它们的高度分别是9m和15m,从建筑物AB的顶部A看建筑物CD的张角∠CAD=45°.
如图,两座建筑物AB,CD的底部都在同一个水平面上,且均与水平面垂直,它们的高度分别是9m和15m,从建筑物AB的顶部A看建筑物CD的张角∠CAD=45°.(1)求BC的长度;
(2)在线段BC上取一点P(点P与点B,C不重合),从点P看这两座建筑物的张角分别为∠APB=α,∠DPC=β,问点P在何处时,tan(α+β)最小?
考点:解三角形的实际应用
专题:应用题,解三角形
分析:(1)作AN⊥CD于N,问题转化为求△ACD边CD上的高.设AN=x,只要建立起关于x的方程,则问题可解.
(2)利用(1)设出BP为t,直接求出α、β的正切值,然后求出∠ADB的正切值,利用基本不等式求解表达式的最小值,推出BP是值即可.
(2)利用(1)设出BP为t,直接求出α、β的正切值,然后求出∠ADB的正切值,利用基本不等式求解表达式的最小值,推出BP是值即可.
解答:
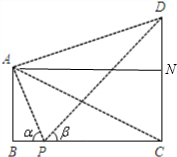 解:(1)如图作AN⊥CD于N.
解:(1)如图作AN⊥CD于N.
∵AB∥CD,AB=9,CD=15,∴DN=6,NC=9.
设AN=x,∠DAN=θ,
∵∠CAD=45°,∴∠CAN=45°-θ.
在Rt△ANC和Rt△AND中,
∵tanθ=
,tan(45°-θ)=
∴
=tan(45°-θ)=
代入化简整理得x2-15x-54=0,
解得x1=18,x2=-3(舍去).
∴BC的长度是18m.
(2)设BP=t,则PC=18-t,tanα=
,tanβ=
,
∴tan(α+β)=
=
=-
≥-
,
当且仅当t+27=
,即t=15
-27时,tan(α+β)最小.
即P在距离B15
-27m时,tan(α+β)最小.
 解:(1)如图作AN⊥CD于N.
解:(1)如图作AN⊥CD于N.∵AB∥CD,AB=9,CD=15,∴DN=6,NC=9.
设AN=x,∠DAN=θ,
∵∠CAD=45°,∴∠CAN=45°-θ.
在Rt△ANC和Rt△AND中,
∵tanθ=
| 6 |
| x |
| 9 |
| x |
∴
| 9 |
| x |
| 1-tanθ |
| 1+tanθ |
代入化简整理得x2-15x-54=0,
解得x1=18,x2=-3(舍去).
∴BC的长度是18m.
(2)设BP=t,则PC=18-t,tanα=
| 9 |
| t |
| 15 |
| 18-t |
∴tan(α+β)=
| tanα+tanβ |
| 1-tanαtanβ |
| ||||
1-
|
| 6 | ||
t+27+
|
| 6 | ||
2
|
当且仅当t+27=
| 1350 |
| t+27 |
| 6 |
即P在距离B15
| 6 |
点评:考查了解三角形的实际应用.解这类题的关键是建立数学模型,设出恰当的角.考查两角和与差的三角函数,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
复数
的共轭复数对应的点在复平面的( )
| 5 |
| i-2 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |