题目内容
一批型号相同的产品,有2件次品,5件正品,每次抽一件测试,直到将两件次品全部区分为止.假设抽后不放回,则第5次测试后停止的概率是 .
考点:相互独立事件的概率乘法公式
专题:概率与统计
分析:第5次测试后2件次品全部测出,故第五次抽出的为次品,前四次抽取的有3件正品,一件次品.故只需考虑前5件的排列问题.用古典概型求解即可.
解答:
解:第5次测试后停止,说明前4次抽到1个次品和3件正品,第5次抽到次品,
故概率为P=C41×
×
×
×
+×
×
×
×
×
=
,
故答案为:
.
故概率为P=C41×
| 5 |
| 7 |
| 4 |
| 6 |
| 3 |
| 5 |
| 2 |
| 4 |
| 5 |
| 7 |
| 4 |
| 6 |
| 3 |
| 5 |
| 2 |
| 4 |
| 1 |
| 3 |
| 5 |
| 21 |
故答案为:
| 5 |
| 21 |
点评:本题考查古典概型问题,考查分析问题、解决问题的能力,属于基础题.

练习册系列答案
相关题目
双曲线x2-y2=2的顶点到其渐进线的距离等于( )
A、
| ||||
B、
| ||||
| C、1 | ||||
D、
|
已知一个算法,其流程图如图所示,若输入a=3,b=4,则输出的结果是( )

A、
| ||
| B、6 | ||
| C、7 | ||
| D、12 |
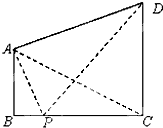 如图,两座建筑物AB,CD的底部都在同一个水平面上,且均与水平面垂直,它们的高度分别是9m和15m,从建筑物AB的顶部A看建筑物CD的张角∠CAD=45°.
如图,两座建筑物AB,CD的底部都在同一个水平面上,且均与水平面垂直,它们的高度分别是9m和15m,从建筑物AB的顶部A看建筑物CD的张角∠CAD=45°.