题目内容
已知数列{an}满足a2=
,an=
(1-an-1),求数列{an}的通项公式.
| 1 |
| 3 |
| 1 |
| 3 |
考点:数列递推式
专题:点列、递归数列与数学归纳法
分析:由数列递推式结合a2=
求得a1,再由数列递推式构造出等比数列{an-
},求出其通项公式,则数列{an}的通项公式可求.
| 1 |
| 3 |
| 1 |
| 4 |
解答:
解:由an=
(1-an-1),得an=-
an-1+
,
即an-
=-
(an-1-
),
再由a2=
,an=
(1-an-1),得a1=0,
∴a1-
=-
.
∴数列{an-
}是以-
为首项,以-
为公比的等比数列.
则an-
=-
×(-
)n-1,
∴an=
-
×(-
)n-1.
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
即an-
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 4 |
再由a2=
| 1 |
| 3 |
| 1 |
| 3 |
∴a1-
| 1 |
| 4 |
| 1 |
| 4 |
∴数列{an-
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 3 |
则an-
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 3 |
∴an=
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 3 |
点评:本题考查了数列递推式,考查了等比关系的确定,是中档题.

练习册系列答案
相关题目
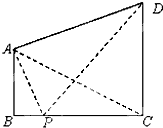 如图,两座建筑物AB,CD的底部都在同一个水平面上,且均与水平面垂直,它们的高度分别是9m和15m,从建筑物AB的顶部A看建筑物CD的张角∠CAD=45°.
如图,两座建筑物AB,CD的底部都在同一个水平面上,且均与水平面垂直,它们的高度分别是9m和15m,从建筑物AB的顶部A看建筑物CD的张角∠CAD=45°.