题目内容
已知等差数列{an}单调递增,a1=1,且a2,a3+4,2a7+1构成等比数列.
(1)求数列{an}的公差d;
(2)设数列{an}的前n项和为Sn,求证:
+
+
+…+
<2(n∈N,且n>1).
(1)求数列{an}的公差d;
(2)设数列{an}的前n项和为Sn,求证:
| 1 |
| S1 |
| 1 |
| S2 |
| 1 |
| S3 |
| 1 |
| Sn |
考点:数列与不等式的综合,等比关系的确定,等差数列的性质
专题:等差数列与等比数列
分析:(1)由等差数列的通项公式和等比数列的性质,即可求出公差,注意公差大于0;
(2)求出前n项和Sn=n2,得到
<
=
-
(n>1),再求和即可证得,注意n的取值.
(2)求出前n项和Sn=n2,得到
| 1 |
| Sn |
| 1 |
| n(n-1) |
| 1 |
| n-1 |
| 1 |
| n |
解答:
(1)解:∵等差数列{an}单调递增,∴an=a1+(n-1)d(d>0)
∵a2,a3+4,2a7+1构成等比数列.∴a2(2a7+1)=(a3+4)2,
即(1+d)(3+12d)=(5+2d)2,解得d=2(负值舍去)
数列{an}的公差d为2;
(2)证明:∵Sn=na1+
n(n-1)d=n+n(n-1)=n2,
∴
=
<
=
-
(n>1)
∴
+
+
+…+
<1+1-
+
-
+
-
+…+
-
=2-
<2(n∈N,且n>1).
∵a2,a3+4,2a7+1构成等比数列.∴a2(2a7+1)=(a3+4)2,
即(1+d)(3+12d)=(5+2d)2,解得d=2(负值舍去)
数列{an}的公差d为2;
(2)证明:∵Sn=na1+
| 1 |
| 2 |
∴
| 1 |
| Sn |
| 1 |
| n2 |
| 1 |
| n(n-1) |
| 1 |
| n-1 |
| 1 |
| n |
∴
| 1 |
| S1 |
| 1 |
| S2 |
| 1 |
| S3 |
| 1 |
| Sn |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n-1 |
| 1 |
| n |
| 1 |
| n |
点评:本题主要考查等差数列和等比数列的通项和性质,以及等差数列的求和公式,放缩法证明不等式,同时考查运用裂项相消求数列的和,注意n的取值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
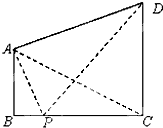 如图,两座建筑物AB,CD的底部都在同一个水平面上,且均与水平面垂直,它们的高度分别是9m和15m,从建筑物AB的顶部A看建筑物CD的张角∠CAD=45°.
如图,两座建筑物AB,CD的底部都在同一个水平面上,且均与水平面垂直,它们的高度分别是9m和15m,从建筑物AB的顶部A看建筑物CD的张角∠CAD=45°.