题目内容
数列{an}的通项公式是an=n2-7n+6．
（1）这个数列的第4项是多少？
（2）150是不是这个数列的项？若是这个数列的项，它是第几项？
（3）该数列从第几项开始各项都是正数？
（1）这个数列的第4项是多少？
（2）150是不是这个数列的项？若是这个数列的项，它是第几项？
（3）该数列从第几项开始各项都是正数？
考点：数列的函数特性
专题：等差数列与等比数列
分析：数列{an}的通项公式是an=n2-7n+6求解．
解答：
解：（1）∵an=n2-7n+6，
∴a4=42-7×4+6=-6．
∴这个数列的第4项是-6．
（2）解方程n2-7n+6=150，
得n=16，或n=-9，
∵n∈N*，
∴150是这个数列的项，它是第16项．
（3）由an=n2-7n+6≥0，
得n≤1，或n≥6．
∴数列从第7项开始各项都是正数．
∴a4=42-7×4+6=-6．
∴这个数列的第4项是-6．
（2）解方程n2-7n+6=150，
得n=16，或n=-9，
∵n∈N*，
∴150是这个数列的项，它是第16项．
（3）由an=n2-7n+6≥0，
得n≤1，或n≥6．
∴数列从第7项开始各项都是正数．
点评：本题考查数列的通项公式的性质的应用，解题时要认真审题，是基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
将一个白球，两个相同的红球，三个相同的黄球摆放成一排．则白球与黄球不相邻的放法有（ ）
| A、10种 | B、12种 |
| C、14种 | D、16种 |
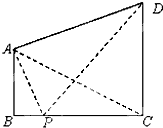如图，两座建筑物AB，CD的底部都在同一个水平面上，且均与水平面垂直，它们的高度分别是9m和15m，从建筑物AB的顶部A看建筑物CD的张角∠CAD=45°．