题目内容
复数
的共轭复数对应的点在复平面的（ ）
| 5 |
| i-2 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
考点：复数代数形式的乘除运算
专题：数系的扩充和复数
分析：利用本题主要考查两个复数代数形式的乘除法，虚数单位i的幂运算性质，化简复数
，可得它的共轭负数以及共轭负数对应的点的坐标，从而得出结论．
| 5 |
| i-2 |
解答：
解：复数
=
=
=-2-i，
它的共轭复数为-2+i，在复平面内的对应点的坐标为（-2，1），
故选：B．
| 5 |
| i-2 |
| 5(-2-i) |
| (-2+i)(-2-i) |
| -10-5i |
| 5 |
它的共轭复数为-2+i，在复平面内的对应点的坐标为（-2，1），
故选：B．
点评：本题主要考查两个复数代数形式的乘除法，虚数单位i的幂运算性质，属于基础题．
练习册系列答案
相关题目
下列函数中，在（0，+∞）上为增函数的是（ ）
A、y=（
| ||
B、y=log
| ||
C、y=
| ||
| D、y=x3 |
双曲线x2-y2=2的顶点到其渐进线的距离等于（ ）
A、
| ||||
B、
| ||||
| C、1 | ||||
D、
|
将一个白球，两个相同的红球，三个相同的黄球摆放成一排．则白球与黄球不相邻的放法有（ ）
| A、10种 | B、12种 |
| C、14种 | D、16种 |
如图，经过AB的平面ABEF与平面ABCD成45°角，经过BE的平面BENM与平面ABEF成30°角，则平面BENM与平面ABCD所成二面角的余弦值为（ ）已知向量
=（1，0），
=（-
，
），则
与
的夹角为（ ）
| a |
| b |
| 1 |
| 2 |
| ||
| 2 |
| a |
| b |
| A、30° | B、60° |
| C、120° | D、150° |
已知一个算法，其流程图如图所示，若输入a=3，b=4，则输出的结果是（ ）
A、
| ||
| B、6 | ||
| C、7 | ||
| D、12 |
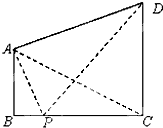如图，两座建筑物AB，CD的底部都在同一个水平面上，且均与水平面垂直，它们的高度分别是9m和15m，从建筑物AB的顶部A看建筑物CD的张角∠CAD=45°．