题目内容
在△ABC中，M、N分别为边AC、AB的中点，∠B=30°，且
•
=
•
，则BC：BA= ．
| BM |
| AC |
| CN |
| AB |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：利用三角形的中线的性质得到
=
(
+
)，
=
(
+
)，将已知等式变形得
•(
+
)=0，设BC的中点为Q，则AQ⊥BC，再结合∠B=30°得到所求．
| BM |
| 1 |
| 2 |
| BA |
| BC |
| CN |
| 1 |
| 2 |
| CA |
| CB |
| BC |
| AC |
| AB |
解答：
解：因为在△ABC中，M、N分别为边AC、AB的中点，
所以
=
(
+
)，
=
(
+
)，
又
•
=
•
，所以
(
+
)•
=
(
+
)•
，整理得
•(
+
)=0，设BC的中点为Q，则AQ⊥BC，
又∠B=30°，所以BC：BA=2BQ：BA=2cos∠B=2×
=
；
故答案为：
．
所以
| BM |
| 1 |
| 2 |
| BA |
| BC |
| CN |
| 1 |
| 2 |
| CA |
| CB |
又
| BM |
| AC |
| CN |
| AB |
| 1 |
| 2 |
| BA |
| BC |
| AC |
| 1 |
| 2 |
| CA |
| CB |
| AB |
| BC |
| AC |
| AB |
又∠B=30°，所以BC：BA=2BQ：BA=2cos∠B=2×
| ||
| 2 |
| 3 |
故答案为：
| 3 |
点评：本题考查了三角形的中线性质以及向量垂直数量积为0的运用．
练习册系列答案
名校课堂系列答案
相关题目
已知m和n是两条不同的直线，α和β是两个不重合的平面，则下列给出的条件中，一定能推出m⊥β的是（ ）
| A、α⊥β且m?α |
| B、α⊥β且m∥α |
| C、m∥n且n⊥β |
| D、m⊥n且n∥β； |
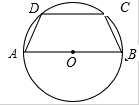四边形ABCD是⊙O的内接等腰梯形，AB为直径，且AB=4．设∠BOC=θ，ABCD的周长为L．