题目内容
二项式(2-x)5展开式中x3的系数是 .
考点:二项式系数的性质
专题:二项式定理
分析:根据二项式(2-x)5展开式的通项公式,求出x3的系数即可.
解答:
解:∵二项式(2-x)5展开式的通项公式是
Tr+1=
•25-r•(-x)r,
令r=3,
∴T3+1=
•22•(-x)3;
∴x3的系数是
•22•(-1)3=-40.
故答案为:-40.
Tr+1=
| C | r 5 |
令r=3,
∴T3+1=
| C | 3 5 |
∴x3的系数是
| C | 3 5 |
故答案为:-40.
点评:本题考查了二项式展开式的通项公式的应用问题,是基础题目.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
设x、y满足约束条件
,则z=x+y的最大值为( )
|
| A、2 | ||
B、
| ||
C、
| ||
| D、1 |
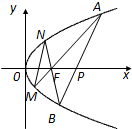 如图,已知抛物线y2=4x的焦点为F,过点P(2,0)且斜率为k1的直线交抛物线于A(x1,y1),B(x2,y2)两点,直线AF、BF分别与抛物线交于点M、N.
如图,已知抛物线y2=4x的焦点为F,过点P(2,0)且斜率为k1的直线交抛物线于A(x1,y1),B(x2,y2)两点,直线AF、BF分别与抛物线交于点M、N.