题目内容
设P(x,y)是角θ的终边上任意一点,其中x≠0,y≠0,并记r=
.若定义cotθ=
,secθ=
,cscθ=
.
(Ⅰ)求证sin2θ+cos2θ-tan2θ-cot2θ+sec2θ+csc2θ是一个定值,并求出这个定值;
(Ⅱ)求函数f(θ)=|sinθ+cosθ+tanθ+cotθ+secθ+cscθ|的最小值.
| x2+y2 |
| x |
| y |
| r |
| x |
| r |
| y |
(Ⅰ)求证sin2θ+cos2θ-tan2θ-cot2θ+sec2θ+csc2θ是一个定值,并求出这个定值;
(Ⅱ)求函数f(θ)=|sinθ+cosθ+tanθ+cotθ+secθ+cscθ|的最小值.
考点:任意角的三角函数的定义
专题:计算题,三角函数的求值
分析:(Ⅰ)直接利用三角函数基本关系式,以及三角函数的定义化简表达式sin2θ+cos2θ-tan2θ-cot2θ+sec2θ+csc2θ,求解即可;
(Ⅱ)利用已知条件化简函数f(θ)=|sinθ+cosθ+tanθ+cotθ+secθ+cscθ|题干基本不等式求出函数的最小值.
(Ⅱ)利用已知条件化简函数f(θ)=|sinθ+cosθ+tanθ+cotθ+secθ+cscθ|题干基本不等式求出函数的最小值.
解答:
解:(Ⅰ)sin2θ+cos2θ-tan2θ-cot2θ+sec2θ+csc2θ
=1-(
)2-(
)2+(
)2+(
)2
=1+1+1=3…(4分)
(Ⅱ)由条件,cotθ=
=tanθ,secθ=
,cscθ=
令g(θ)=sinθ+cosθ+tanθ+cotθ+secθ+cscθ=sinθ+cosθ+
+
+
+
=sinθ+cosθ+
+
…(6分)
令sinθ+cosθ=t,则t=sinθ+cosθ=
sin(θ+
)∈[-
,
],t≠±1,且sinθcosθ=
,
从而g(θ)=y=t+
+
=t+
=t+
=t-1+
+1,…(9分)
令u=t-1,则y=u+
+1,u∈[-
-1,
-1],且t≠0,t≠-2.
∴y∈(-∞,1-2
]∪[3
+2,+∞).
从而f(θ)=|y|≥2
-1,即f(θ)min=2
-1. …(12分)
=1-(
| y |
| x |
| x |
| y |
| r |
| x |
| r |
| y |
=1+1+1=3…(4分)
(Ⅱ)由条件,cotθ=
| x |
| y |
| 1 |
| cosx |
| 1 |
| sinθ |
令g(θ)=sinθ+cosθ+tanθ+cotθ+secθ+cscθ=sinθ+cosθ+
| sinθ |
| cosθ |
| cosθ |
| sinθ |
| 1 |
| cosθ |
| 1 |
| sinθ |
| 1 |
| sinθcosθ |
| sinθ+cosθ |
| sinθcosθ |
令sinθ+cosθ=t,则t=sinθ+cosθ=
| 2 |
| π |
| 4 |
| 2 |
| 2 |
| t2-1 |
| 2 |
从而g(θ)=y=t+
| 2 |
| t2-1 |
| 2t |
| t2-1 |
| 2(t+1) |
| t2-1 |
| 2 |
| t-1 |
| 2 |
| t-1 |
令u=t-1,则y=u+
| 2 |
| u |
| 2 |
| 2 |
∴y∈(-∞,1-2
| 2 |
| 2 |
从而f(θ)=|y|≥2
| 2 |
| 2 |
点评:本题考查任意角的三角函数的定义以及应用,基本知识的考查.

练习册系列答案
相关题目
已知△ABC内接于圆O(圆心是三边垂直平分线的交点),若
•
=2
•
,且|AB|=3,|CA|=6,则cosA的值是( )
| CO |
| AB |
| BO |
| CA |
A、
| ||||
B、
| ||||
C、-
| ||||
D、
|
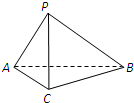 如图,在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC.
如图,在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC.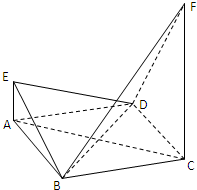 已知四边形ABCD是菱形,其对角线AC=4,BD=2,直线AE,CF都与平面ABCD垂直,AE=1,CF=4.
已知四边形ABCD是菱形,其对角线AC=4,BD=2,直线AE,CF都与平面ABCD垂直,AE=1,CF=4. 如图所示,在长方体ABCD-A1B1C1D1中,AA1=2,AB=AD=1,点M是CC1的中点,
如图所示,在长方体ABCD-A1B1C1D1中,AA1=2,AB=AD=1,点M是CC1的中点,