题目内容
函数f(x)定义在区间(0,+∞),y∈R,都有f(xy)=yf(x),且f(x)不恒为零.
(1)求f(1)的值;
(2)若a>b>c>1且b2=ac,求证:f(a)f(c)<[f(b)]2;
(3)若f(
)<0,求证:f(x)在(0,+∞)上是增函数.
(1)求f(1)的值;
(2)若a>b>c>1且b2=ac,求证:f(a)f(c)<[f(b)]2;
(3)若f(
| 1 |
| 2 |
考点:抽象函数及其应用,函数单调性的判断与证明
专题:函数的性质及应用
分析:(1)利用赋值法即可求f(1)的值;
(2)根据不等式的性质即可证明不等式f(a)f(c)<[f(b)]2;
(3)由条件f(
)<0,根据单调性的定义即可证明f(x)在(0,+∞)上是增函数.
(2)根据不等式的性质即可证明不等式f(a)f(c)<[f(b)]2;
(3)由条件f(
| 1 |
| 2 |
解答:
(1)令x=1,y=2,可知f(1)=2f(1),故f(1)=0,
(2)设xy=ac,则y=log?xac,
∴f(ac)=f(xy)=yf(x)=(log?xac)f(x)=(log?xa+log?xc)f(x)=(log?xa)f(x)+(log?xc)f(x)=f(xlog?xa)+f(xlog?xc)=f(a)+f(c),
∵b2=ac,
∴f(b2)=f(ac),
即2f(b)=f(a)+f(c),
f(b)=
,
∴[f(b)]2-f(a)f(c)=[
]2-f(a)f(c)=[
]2≥0.
下面证明当x≠1时,f(x)≠0.
假设存在x≠1,f(x0)=0,则对于任意x≠1,
f(x)=f[x0logx0x]=(log?x0x)f(x0)=0,不合题意.所以,当x≠1时,f(x)≠0.
因为a>b>c>1,所以存在m≠1,
f(a)-f(c)=f(mlog?ma)-f(mlog?mc)=(log?ma-log?mc)f(m)≠0,
所以f(a)≠f(c),所以f(a)f(c)<f2(b).
(3)设x0∈(0,1),则f(x0)=f[(
)log?
x0]=(log?
x0)f(
)<0,
设x1,x2为区间(0,+∞)内的任意两个值,且x1<x2,则0<
<1,
由(2)的证明知,
f(x1)-f(x2)=f(
×x2)-f(x2)=f(
)+f(x2)-f(x2)=f(
)<0,
所以f(x1)<f(x2),所以f(x)在(0,+∞)上是增函数.
(2)设xy=ac,则y=log?xac,
∴f(ac)=f(xy)=yf(x)=(log?xac)f(x)=(log?xa+log?xc)f(x)=(log?xa)f(x)+(log?xc)f(x)=f(xlog?xa)+f(xlog?xc)=f(a)+f(c),
∵b2=ac,
∴f(b2)=f(ac),
即2f(b)=f(a)+f(c),
f(b)=
| f(a)+f(c) |
| 2 |
∴[f(b)]2-f(a)f(c)=[
| f(a)+f(c) |
| 2 |
| f(a)-f(c) |
| 2 |
下面证明当x≠1时,f(x)≠0.
假设存在x≠1,f(x0)=0,则对于任意x≠1,
f(x)=f[x0logx0x]=(log?x0x)f(x0)=0,不合题意.所以,当x≠1时,f(x)≠0.
因为a>b>c>1,所以存在m≠1,
f(a)-f(c)=f(mlog?ma)-f(mlog?mc)=(log?ma-log?mc)f(m)≠0,
所以f(a)≠f(c),所以f(a)f(c)<f2(b).
(3)设x0∈(0,1),则f(x0)=f[(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
设x1,x2为区间(0,+∞)内的任意两个值,且x1<x2,则0<
| x1 |
| x2 |
由(2)的证明知,
f(x1)-f(x2)=f(
| x1 |
| x2 |
| x1 |
| x2 |
| x1 |
| x2 |
所以f(x1)<f(x2),所以f(x)在(0,+∞)上是增函数.
点评:本题主要考查抽象函数应用以及函数单调性的应用,综合考查学生的运算能力,综合性较强,难度较大.

练习册系列答案
相关题目
已知面α⊥β,α∩β=l,直线a?α,直线b?β,a,b与l斜交,则( )
| A、a和b不垂直但可能平行 |
| B、a和b可能垂直也可能平行 |
| C、a和b不平行但可能垂直 |
| D、a和b既不垂直也不平行 |
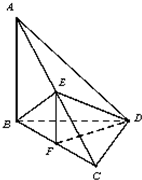 如图,已知三棱锥A-BCD,AB⊥BD,AD⊥CD,E,F分别为AC,BC的中点,且△BEC为正三角形.
如图,已知三棱锥A-BCD,AB⊥BD,AD⊥CD,E,F分别为AC,BC的中点,且△BEC为正三角形.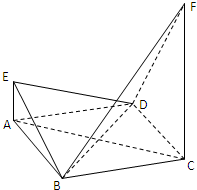 已知四边形ABCD是菱形,其对角线AC=4,BD=2,直线AE,CF都与平面ABCD垂直,AE=1,CF=4.
已知四边形ABCD是菱形,其对角线AC=4,BD=2,直线AE,CF都与平面ABCD垂直,AE=1,CF=4.