题目内容
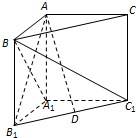 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1.
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1.(Ⅰ)求证:AB1⊥平面A1BC1;
(Ⅱ)若D为B1C1的中点,求AD与平面A1B1C1所成角的正弦值.
考点:直线与平面所成的角,直线与平面垂直的判定
专题:计算题,空间位置关系与距离,空间角
分析:(I)根据AA1⊥平面A1B1C1证出AA1⊥A1C1,结合A1C1⊥A1B1得到A1C1⊥平面AA1B1B,从而证出AB1⊥A1C1.然后在正方形AA1B1B中证出AB1⊥A1B,可得出AB1⊥平面A1BC1;
(II)连结AD,由AA1⊥平面A1B1C1可得∠A1DA是AD与平面A1B1C1所成角.然后在Rt△A1DA中利用解直角三角形加以计算,可得AD与平面A1B1C1所成角的正弦值.
(II)连结AD,由AA1⊥平面A1B1C1可得∠A1DA是AD与平面A1B1C1所成角.然后在Rt△A1DA中利用解直角三角形加以计算,可得AD与平面A1B1C1所成角的正弦值.
解答:
解:(I)∵直三棱柱ABC-A1B1C1中,AA1⊥平面A1B1C1,A1C1?平面A1B1C1,
∴AA1⊥A1C1,
又∵∠B1A1C1=90°,即A1C1⊥A1B1,A1B1、AA1是平面AA1B1B内的相交直线,
∴A1C1⊥平面AA1B1B,可得AB1⊥A1C1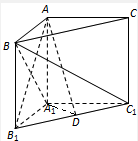
∵直三棱柱ABC-A1B1C1中,AB=AC=AA1,
∴四边形AA1B1B是正方形,可得AB1⊥A1B,
又∵A1B、A1C1是平面A1BC1内的相交直线,
∴AB1⊥平面A1BC1;
(II)连结AD,设AB=AC=AA1=1,
∵AA1⊥平面A1B1C1,∴∠A1DA是AD与平面A1B1C1所成角
∵等腰Rt△A1B1C1中,D为斜边的中点,∴A1D=
B1C1=
,
又∵Rt△A1DA中,AD=
=
,
∴sin∠A1DA=
=
,即AD与平面A1B1C1所成角的正弦值等于
.
∴AA1⊥A1C1,
又∵∠B1A1C1=90°,即A1C1⊥A1B1,A1B1、AA1是平面AA1B1B内的相交直线,
∴A1C1⊥平面AA1B1B,可得AB1⊥A1C1

∵直三棱柱ABC-A1B1C1中,AB=AC=AA1,
∴四边形AA1B1B是正方形,可得AB1⊥A1B,
又∵A1B、A1C1是平面A1BC1内的相交直线,
∴AB1⊥平面A1BC1;
(II)连结AD,设AB=AC=AA1=1,
∵AA1⊥平面A1B1C1,∴∠A1DA是AD与平面A1B1C1所成角
∵等腰Rt△A1B1C1中,D为斜边的中点,∴A1D=
| 1 |
| 2 |
| ||
| 2 |
又∵Rt△A1DA中,AD=
| A1D2+A1A 2 |
| ||
| 2 |
∴sin∠A1DA=
| A1D |
| AD |
| ||
| 3 |
| ||
| 3 |
点评:本题在特殊的三棱柱中求证线面垂直,并求直线与平面所成角的大小.着重考查了直三棱柱的性质、线面垂直的判定与性质和直线与平面所成角的求法等知识,属于中档题.

练习册系列答案
相关题目
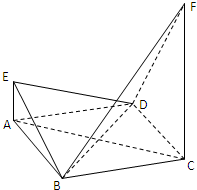 已知四边形ABCD是菱形,其对角线AC=4,BD=2,直线AE,CF都与平面ABCD垂直,AE=1,CF=4.
已知四边形ABCD是菱形,其对角线AC=4,BD=2,直线AE,CF都与平面ABCD垂直,AE=1,CF=4.