题目内容

已知命题p：关于x的不等式x2-2ax+4＞0对一切x∈R恒成立；命题q：函数y=log（4-2a）x在（0，+∞）上递减．若p∨q为真，p∧q为假，求实数a的取值范围．
考点：复合命题的真假
专题：简易逻辑
分析：本题的关键是给出命题p：关于x的不等式x2-2ax+4＞0对一切x∈R恒成立；命题q：函数y=log（4-2a）x在（0，+∞）上递减为真时a的取值范围，在根据p、q一真一假给出a 的取值范围
解答： 解：∵命题p：关于x的不等式x2-2ax+4＞0对一切x∈R恒成立
∴若p为真，△=4a2-16＜0，解得
-2＜a＜2
又∵命题q：函数y=log（4-2a）x在（0，+∞）上递减，
∴若q为真，0＜4-2a＜1，解得
3
2
＜a＜2
∵若p∨q为真，p∧q为假
∴p、q一真一假
①p真q假，
-2＜a＜2
a≤
3
2
或a≥2

②p假q真，
a≤-2或a≥2
3
2
＜a＜2

综上，a 的取值范围：a≤-2或a＞
3
2
．
点评：本题考查的知识点是复合命题的真假判定，解决的办法是先判断组成复合命题的简单命题的真假，再根据真值表进行判断
练习册系列答案
相关题目
已知椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)左顶点C，A为椭圆在第一象限的点，直线OA交椭圆于另一点B，椭圆的左焦点为F1，若直线AF1交BC于M，且
BM
=2
MC
，则椭圆的离心率为（　　）
A、
1
3
B、
1
2
C、
3
3
D、
2
2
已知
a
=（1，1），
b
=（2，3），当k为何值时，
（1）k
a
+2
b
与2
a
-4
b
垂直？
（2）k
a
+2
b
与2
a
-4
b
平行？平行时它们是同向还是反向？
已知函数f（x）=（a2+8）ex，函数g（x）=（x2+ax-2a-3）e3-x．
（1）若a=0，求g（x）的单调递增区间；
（2）若a＞0，且存在ξ1，ξ2∈[0，4]使得|f（ξ1）-g（ξ2）|min＜3，求实数a的取值范围．
设计一个计算1+2+3+…+50的值的算法，并画出程序框图．
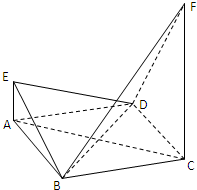已知四边形ABCD是菱形，其对角线AC=4，BD=2，直线AE，CF都与平面ABCD垂直，AE=1，CF=4．
（1）求证：平面EBD⊥平面FBD；
（2）求直线AB与平面EAD所成角的正弦值；
（3）求四棱锥E-ABCD与四棱锥F-ABCD公共部分的体积．
已知A（2，0），B（0，2），C（cosα，sinα），（0＜α＜π）．
（1）若|
OA
+
OC
|=
7
（O为坐标原点），求
OB
与
OC
的夹角；
（2）若
AC
⊥
BC
，求sinα-cosα的值．
已知函数f(x)=cosx(
3
cosx-sinx)-
3
2
．求：
（Ⅰ）函数y=f（x）的对称轴方程；
（Ⅱ）函数y=f（x）在区间[0，
π
2
]上的最值．
二面角α-l-β大小为60°，半平面α、β内分别有点A、B，AC⊥l于C、BD⊥l于D，已知AC=4、CD=5，DB=6，求线段AB的长．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网