题目内容
已知中心在原点,对称轴为坐标轴的双曲线C,一条渐近线方程为x-2y=0,且双曲线经过点A(2
,1).
(1)求双曲线C的方程;
(2)设双曲线C的两个焦点分别为F1,F2,过点P(0,t)作双曲线C切线,切点为M,若△F1MF2的面积为
,求实数t的值.
| 2 |
(1)求双曲线C的方程;
(2)设双曲线C的两个焦点分别为F1,F2,过点P(0,t)作双曲线C切线,切点为M,若△F1MF2的面积为
| ||
| 2 |
考点:直线与圆锥曲线的关系,双曲线的标准方程
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)根据双曲线的一条渐近线方程为x-2y=0,可设双曲线C的方程x2-4y2=λ,代入点A(2
,1),可得双曲线C的方程;
(2)利用△F1MF2的面积为
,求出M的坐标,求导数,得到切线的向量,即可求实数t的值.
| 2 |
(2)利用△F1MF2的面积为
| ||
| 2 |
解答:
解:(1)∵双曲线的一条渐近线方程为x-2y=0,
∴可设双曲线C的方程x2-4y2=λ,
∵双曲线经过点A(2
,1),
∴8-4=λ,
∴λ=4,
∴双曲线C的方程为
-y2=1;
(2)双曲线C的两个焦点分别为F1(-
,0),F2(
,0),∴|F1F2|=2
.
设M(x,y),则∵△F1MF2的面积为
,
∴
•2
•|y|=
,
∴|y|=
,
∴|x|=
,
取点M(
,
),则PM的方程为y=
x+t,
由
-y2=1,可得y=
,∴y′=
,
x=
时,y′=
,
∴
=
,
∴t=-2,
同理,根据对称性,可得t=2.
∴可设双曲线C的方程x2-4y2=λ,
∵双曲线经过点A(2
| 2 |
∴8-4=λ,
∴λ=4,
∴双曲线C的方程为
| x2 |
| 4 |
(2)双曲线C的两个焦点分别为F1(-
| 5 |
| 5 |
| 5 |
设M(x,y),则∵△F1MF2的面积为
| ||
| 2 |
∴
| 1 |
| 2 |
| 5 |
| ||
| 2 |
∴|y|=
| 1 |
| 2 |
∴|x|=
| 5 |
取点M(
| 5 |
| 1 |
| 2 |
| ||
|
由
| x2 |
| 4 |
|
| x | ||||
4
|
x=
| 5 |
| ||
| 2 |
∴
| ||
|
| ||
| 2 |
∴t=-2,
同理,根据对称性,可得t=2.
点评:本题考查双曲线的方程与几何性质,考查三角形面积的计算,考查双曲线的切线,考查学生的计算能力,属于中档题.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
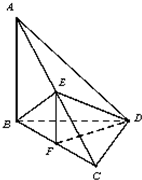 如图,已知三棱锥A-BCD,AB⊥BD,AD⊥CD,E,F分别为AC,BC的中点,且△BEC为正三角形.
如图,已知三棱锥A-BCD,AB⊥BD,AD⊥CD,E,F分别为AC,BC的中点,且△BEC为正三角形.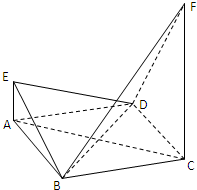 已知四边形ABCD是菱形,其对角线AC=4,BD=2,直线AE,CF都与平面ABCD垂直,AE=1,CF=4.
已知四边形ABCD是菱形,其对角线AC=4,BD=2,直线AE,CF都与平面ABCD垂直,AE=1,CF=4.