题目内容
已知函数f（x）=x2-x-2a
（1）若a=1，求函数f（x）的零点；
（2）若f（x）有零点，求a的范围．
（1）若a=1，求函数f（x）的零点；
（2）若f（x）有零点，求a的范围．
考点：函数的零点,函数零点的判定定理
专题：函数的性质及应用
分析：根据函数零点的定义分别进行求解和判断即可．
解答：
解：（1）当a=1时，f（x）=x2-x-2
令f（x）=x2-x-2=0得x=-1，或x=2
即函数f（x）的零点为-1与2．
（2）要使f（x）有零点
则△=1+8a≥0，
即a≥-
．
∴a≥-
令f（x）=x2-x-2=0得x=-1，或x=2
即函数f（x）的零点为-1与2．
（2）要使f（x）有零点
则△=1+8a≥0，
即a≥-
| 1 |
| 8 |
∴a≥-
| 1 |
| 8 |
点评：本题主要考查二次函数零点的应用，根据二次函数和二次方程之间的关系是解决本题的关键，比较基础．
练习册系列答案
寒假天地重庆出版社系列答案
相关题目
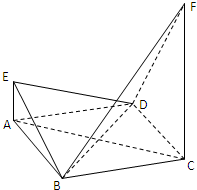已知四边形ABCD是菱形，其对角线AC=4，BD=2，直线AE，CF都与平面ABCD垂直，AE=1，CF=4．
