题目内容
设函数f(x)=|x-a|+3x,(a∈R).
(1)求不等式f(x)>3x+1的解集;
(2)若不等式f(x)≤0的解集为{x|x≤-1},求a的值.
(1)求不等式f(x)>3x+1的解集;
(2)若不等式f(x)≤0的解集为{x|x≤-1},求a的值.
考点:绝对值不等式的解法
专题:计算题,不等式的解法及应用
分析:(1)f(x)>3x+1?|x-a|+3x>3x+1?|x-a|>1,利用绝对值不等式的几何意义即可求得原不等式的解集;
(2)不等式|x-a|+3x≤0等价于3x≤x-a≤-3x,转化为不等式组即
,通过对参数a<0与a≥0的讨论,利用不等式f(x)≤0的解集为{x|x≤-1},即可求得a的值.
(2)不等式|x-a|+3x≤0等价于3x≤x-a≤-3x,转化为不等式组即
|
解答:
解(1)由f(x)>3x+1化简可得|x-a|>1,即x-a>1或x-a<-1,
解得:x>a+1或x<a-1------(2分)
∴不等式f(x)>3x+1的解集为{x|x>a+1或x<a-1}------(4分)
(2)不等式|x-a|+3x≤0等价于3x≤x-a≤-3x,即
即
----(6分)
若a<0则原不等式的解集是{x|x≤
}={x|x≤-1},此时a=-4
若a≥0则原不等式的解集是{x|x≤-
}={x|x≤-1},此时a=2
综上:a=2或a=-4------(10分)
解得:x>a+1或x<a-1------(2分)
∴不等式f(x)>3x+1的解集为{x|x>a+1或x<a-1}------(4分)
(2)不等式|x-a|+3x≤0等价于3x≤x-a≤-3x,即
|
|
若a<0则原不等式的解集是{x|x≤
| a |
| 4 |
若a≥0则原不等式的解集是{x|x≤-
| a |
| 2 |
综上:a=2或a=-4------(10分)
点评:本题考查绝对值不等式的解法,着重考查转化思想与分类讨论思想的综合应用,考查运算求解能力,属于中档题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
下列不等式正确的是( )
| A、若a>b,则a•c>b•c | ||||
| B、若a•c2>b•c2,则a>b | ||||
C、若a>b,则
| ||||
| D、若a>b,则a•c2>b•c2 |
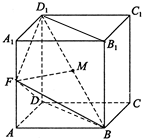 如图,已知在棱柱ABCD-A1B1C1D1的底面是菱形,且AA1⊥面ABCD,∠DAB=60°,AD=AA1=1,F为棱AA1的中点,M为线段BD1的中点.
如图,已知在棱柱ABCD-A1B1C1D1的底面是菱形,且AA1⊥面ABCD,∠DAB=60°,AD=AA1=1,F为棱AA1的中点,M为线段BD1的中点. 如图,在△ABC中,点D在边BC上,且
如图,在△ABC中,点D在边BC上,且