题目内容
从我校4名男生和3名女生中任选3人参加孝感市迎五四演讲比赛.设随机变量X表示所选3人中女生的人数.
(1)求X的分布列;
(2)求“所选3人中女生人数X≤1”的概率.
(1)求X的分布列;
(2)求“所选3人中女生人数X≤1”的概率.
考点:离散型随机变量及其分布列,互斥事件的概率加法公式
专题:概率与统计
分析:(1)所选的3人中女生随机变量X的所有可能取值为0,1,2,3,p(X=k)=
,k=0,1,2,3,由此能求出X的分布列.
(2)“所选3人中女生人数X≤1”的概率p=p(X=0)+p(X=1),由此能求出结果.
| ||||
|
(2)“所选3人中女生人数X≤1”的概率p=p(X=0)+p(X=1),由此能求出结果.
解答:
解:(1)所选的3人中女生随机变量X的所有可能取值为0,1,2,3,
p(X=k)=
,k=0,1,2,3,
p(X=0)=
=
,p(X=1)=
=
,
p(X=2)=
=
,p(X=4)=
=
.
∴X的分布列为:
(2)由(1)知“所选3人中女生人数X≤1”的概率:
p=p(X=0)+p(X=1)
=
+
=
.
p(X=k)=
| ||||
|
p(X=0)=
| ||||
|
| 4 |
| 35 |
| ||||
|
| 18 |
| 35 |
p(X=2)=
| ||||
|
| 12 |
| 35 |
| ||||
|
| 1 |
| 35 |
∴X的分布列为:
| X | 0 | 1 | 2 | 3 | ||||||||
| p |
|
|
|
|
p=p(X=0)+p(X=1)
=
| 4 |
| 35 |
| 18 |
| 35 |
| 22 |
| 35 |
点评:本题考查概率的求法,考查离散型随机变量的分布列的求法,是中档题,在历年高考中都是必考题型之一.

练习册系列答案
相关题目
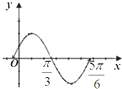
已知函数y=2sin(ωx+φ)(ω>0,|φ|<
)的图象的一部分如图所示,则( )
| π |
| 2 |

A、ω=2,φ=
| ||
B、ω=2,φ=-
| ||
C、ω=2,φ=
| ||
D、ω=2,φ=-
|
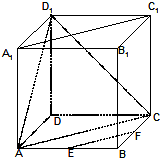 如图,棱长为2的正方体ABCD-A1B1C1D1中,点E,F分别为棱AB,BC的中点.
如图,棱长为2的正方体ABCD-A1B1C1D1中,点E,F分别为棱AB,BC的中点.