题目内容
(2-
)8展开式中
(1)求x4项的系数
(2)求不含x4项的系数的和.
| x |
(1)求x4项的系数
(2)求不含x4项的系数的和.
考点:二项式定理的应用,二项式系数的性质
专题:二项式定理
分析:(1)由题意知利用二项展开式的通项公式写出展开式的通项,令x的指数为4,即可得到结论,
(2)令x=1得到,所有项的系数,然后减去x4项的系数即可得到结论.
(2)令x=1得到,所有项的系数,然后减去x4项的系数即可得到结论.
解答:
解2-
)8的展开式的通项为Tr+1=
28-r•(-
)r=
•(-1)r•28-r•x
,
令
=4,解得r=8,
得到展开式中x4的项为
x4=x4,即x4项的系数是1,
(2)令x=1,则所有项的系数和为(2-1)8=1,
则求不含x4项的系数的和为1-1=0.
| x |
| C | r 8 |
| x |
| C | r 8 |
| r |
| 2 |
令
| r |
| 2 |
得到展开式中x4的项为
| C | 8 8 |
(2)令x=1,则所有项的系数和为(2-1)8=1,
则求不含x4项的系数的和为1-1=0.
点评:本题考查利用二项展开式的通项公式解决二项展开式的特定项问题,本题解题的关键是写出二项式的展开式,所有的这类问题都是利用通项来解决的.

练习册系列答案
相关题目
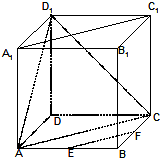 如图,棱长为2的正方体ABCD-A1B1C1D1中,点E,F分别为棱AB,BC的中点.
如图,棱长为2的正方体ABCD-A1B1C1D1中,点E,F分别为棱AB,BC的中点.