题目内容
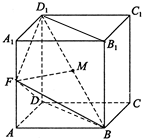 如图,已知在棱柱ABCD-A1B1C1D1的底面是菱形,且AA1⊥面ABCD,∠DAB=60°,AD=AA1=1,F为棱AA1的中点,M为线段BD1的中点.
如图,已知在棱柱ABCD-A1B1C1D1的底面是菱形,且AA1⊥面ABCD,∠DAB=60°,AD=AA1=1,F为棱AA1的中点,M为线段BD1的中点.(1)求证:平面D1FB⊥平面BDD1B1;
(2)求三棱锥D1-BDF的体积.
考点:棱柱、棱锥、棱台的体积,平面与平面垂直的判定
专题:空间位置关系与距离
分析:(1)由底面是菱形,证明AC⊥面BDD1B1,再证MF⊥面BDD1B1,即证平面D1FB⊥平面BDD1B1;
(2)过点B作BH⊥AD于H,可证出BH⊥平面ADD1A1,从而BH是三棱锥B-DD1F的高,求出△DD1F的面积,计算出三棱锥D1-BDF的体积.
(2)过点B作BH⊥AD于H,可证出BH⊥平面ADD1A1,从而BH是三棱锥B-DD1F的高,求出△DD1F的面积,计算出三棱锥D1-BDF的体积.
解答:
 解:(1)证明:∵底面是菱形,
解:(1)证明:∵底面是菱形,
∴AC⊥BD;
又∵B1B⊥面ABCD,AC?面ABCD
∴AC⊥B1B,BD∩B1B=B,
∴AC⊥面BDD1B1
又∵MF∥AC,
∴MF⊥面BDD1B1;
又∵MF?平面D1FB,
∴平面D1FB⊥平面BDD1B1;
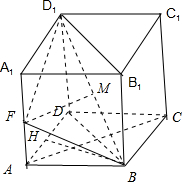
(2)如图,过点B作BH⊥AD,垂足为H,
∵AA1⊥平面ABCD,BH⊆平面ABCD,
∴BH⊥AA1,
∵AD、AA1是平面ADD1A1内的相交直线,
∴BH⊥平面ADD1A1,
在Rt△ABH中,∠DAB=60°,AB=AD=1,
∴BH=ABsin60°=
,
∴三棱锥D1-BDF的体积为
V=V三棱锥B-D1DF=
×S△DD1F•BH=
×
×1×1×
=
.
 解:(1)证明:∵底面是菱形,
解:(1)证明:∵底面是菱形,∴AC⊥BD;
又∵B1B⊥面ABCD,AC?面ABCD
∴AC⊥B1B,BD∩B1B=B,
∴AC⊥面BDD1B1
又∵MF∥AC,
∴MF⊥面BDD1B1;
又∵MF?平面D1FB,
∴平面D1FB⊥平面BDD1B1;
(2)如图,过点B作BH⊥AD,垂足为H,
∵AA1⊥平面ABCD,BH⊆平面ABCD,
∴BH⊥AA1,
∵AD、AA1是平面ADD1A1内的相交直线,
∴BH⊥平面ADD1A1,
在Rt△ABH中,∠DAB=60°,AB=AD=1,
∴BH=ABsin60°=
| ||
| 2 |
∴三棱锥D1-BDF的体积为
V=V三棱锥B-D1DF=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 12 |
点评:点评:本题考查了空间中的垂直关系的证明问题与求锥体的条件问题,解题时应借助于几何图形进行解答,是易错题.

练习册系列答案
相关题目