题目内容
1.下列命题为真命题的个数是( )①?x∈{x|x是无理数},x2是无理数;
②命题“?x0∈R,${x}_{0}^{2}$+1>3x0”的否定是“?x∈R,x2+1≤3x”;
③命题“若x2+y2=0,x∈R,y∈R,则x=y=0”的逆否命题为真命题;
④(2e-x)′=2e-x.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 ①,比如当x=$\sqrt{2}$时,就不成立;
②,命题“?x0∈R,${x}_{0}^{2}$+1>3x0”的否定是“?x∈R,x2+1≤3x”;
③,命题“若x2+y2=0,x∈R,y∈R,则x=y=0”为真命题,其逆否命题为真命题;
④,(2e-x)′=-2e-x.
解答 解:对于①,比如当x=$\sqrt{2}$时,就不成立,故错;
对于②,命题“?x0∈R,${x}_{0}^{2}$+1>3x0”的否定是“?x∈R,x2+1≤3x”,正确;
对于③,命题“若x2+y2=0,x∈R,y∈R,则x=y=0”为真命题,其逆否命题为真命题,正确;
对于④,(2e-x)′=-2e-x,故错.
故选:B
点评 本题考查了命题真假的判断,属于基础题.

练习册系列答案
相关题目
9.已知△ABC,AB=4,BC=3,AC=5,现以AB为轴旋转一周,则所得几何体的表面积( )
| A. | 24π | B. | 21 π | C. | 33π | D. | 39 π |
13.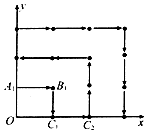 某地区为了绿化环境进行大面积植树造林,如图所示,在区域{(x,y)|x≥0,y≥0}内植树,第1棵树在点A1(0,1)处,第2棵树在点B1(1,1)处,第3棵树在点C1(1,0)处,第4棵树在点C2(2,0)处,接着按图中箭头方向每隔1个单位种1棵树.第n棵树所在点的坐标是(46,0),则n=( )
某地区为了绿化环境进行大面积植树造林,如图所示,在区域{(x,y)|x≥0,y≥0}内植树,第1棵树在点A1(0,1)处,第2棵树在点B1(1,1)处,第3棵树在点C1(1,0)处,第4棵树在点C2(2,0)处,接着按图中箭头方向每隔1个单位种1棵树.第n棵树所在点的坐标是(46,0),则n=( )
 某地区为了绿化环境进行大面积植树造林,如图所示,在区域{(x,y)|x≥0,y≥0}内植树,第1棵树在点A1(0,1)处,第2棵树在点B1(1,1)处,第3棵树在点C1(1,0)处,第4棵树在点C2(2,0)处,接着按图中箭头方向每隔1个单位种1棵树.第n棵树所在点的坐标是(46,0),则n=( )
某地区为了绿化环境进行大面积植树造林,如图所示,在区域{(x,y)|x≥0,y≥0}内植树,第1棵树在点A1(0,1)处,第2棵树在点B1(1,1)处,第3棵树在点C1(1,0)处,第4棵树在点C2(2,0)处,接着按图中箭头方向每隔1个单位种1棵树.第n棵树所在点的坐标是(46,0),则n=( )| A. | 1936 | B. | 2016 | C. | 2017 | D. | 2208 |
11.如图,该算法输出的结果是( )


| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{5}$ |
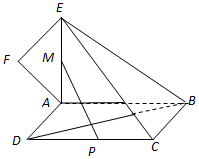 如图,正方形ABCD所在平面与四边形ABEF所在平面互相垂直,△ABE是等腰直角三角形,AB=AE,FA=FE,∠AEF=45°.
如图,正方形ABCD所在平面与四边形ABEF所在平面互相垂直,△ABE是等腰直角三角形,AB=AE,FA=FE,∠AEF=45°.