Question

10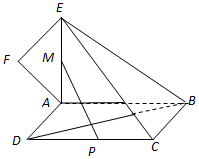．如图，正方形ABCD所在平面与四边形ABEF所在平面互相垂直，△ABE是等腰直角三角形，AB=AE，FA=FE，∠AEF=45°．
（1）求证：EF⊥平面BCE；
（2）设线段CD、AE的中点分别为P、M，求PM与BC所成角的正弦值；
（3）求二面角F-BD-A的平面角的正切值．

Answer 1

分析 （1）证明BC⊥EF．EF⊥BE．然后证明EF⊥平面BCE．
（2）取BE的中点N，连结CN，MN，证明PM∥CN．说明CN与BC所成角∠NCB即为所求，在直角三角形NBC中，求解$sin∠NCB=\frac{{\sqrt{3}}}{3}$．
（3）说明∠FHG为二面角F-BD-A的平面角．设AB=1，则AE=1，在Rt△BGH中与在Rt△FGH中，求解二面角F-BD-A的平面角的正切值．

解答 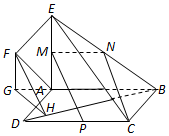（本小题满分12分）
解：（1）因为平面ABEF⊥平面ABCD，BC?平面ABCD，BC⊥AB，
平面ABEF∩平面ABCD=AB，所以BC⊥平面ABEF．所以BC⊥EF．
因为△ABE为等腰直角三角形，AB=AE，
所以∠AEB=45°又因为∠AEF=45°，
所以∠FEB=45°+45°=90°，即EF⊥BE．
因为BC?平面BCE，BE?平面BCE，BC∩BE=B，所以EF⊥平面BCE．
（2）取BE的中点N，连结CN，MN，
则$MN\underline{\underline{∥}}\frac{1}{2}AB\underline{\underline{∥}}PC$，
所以PMNC为平行四边形，所以PM∥CN．
所以CN与BC所成角∠NCB即为所求，正方形ABCD所在平面与四边形ABEF所在平面互相垂直，△ABE是等腰直角三角形，AB=AE，设AE=a，BE=$\frac{\sqrt{2}}{2}a$．BC=a，NC=$\sqrt{1+\frac{1}{2}}a$=$\frac{\sqrt{6}}{2}a$，在直角三角形NBC中，
$sin∠NCB=\frac{{\sqrt{3}}}{3}$．
（3）由EA⊥AB，平面ABEF⊥平面ABCD，易知，EA⊥平面ABCD．
作FG⊥AB，交BA的延长线于G，则FG∥EA．从而，FG⊥平面ABCD．
作GH⊥BD于H，连结FH，则由三垂线定理知，BD⊥FH．
因此，∠FHG为二面角F-BD-A的平面角．
因为FA=FE，∠AEF=45°，所以∠AFE=90°，∠FAG=45°．
设AB=1，则AE=1，$AF=\frac{{\sqrt{2}}}{2}$． $FG=AF•sinFAG=\frac{1}{2}$．
在Rt△BGH中，∠GBH=45°，$BG=AB+AG=1+\frac{1}{2}=\frac{3}{2}$，$GH=BG•sinGBH=\frac{3}{2}•\frac{{\sqrt{2}}}{2}=\frac{{3\sqrt{2}}}{4}$．在Rt△FGH中，$tanFHG=\frac{FG}{GH}=\frac{{\sqrt{2}}}{3}$．
故二面角F-BD-A的平面角的正切值为$tanFHG=\frac{FG}{GH}=\frac{{\sqrt{2}}}{3}$．

点评 本题考查直线与平面垂直的判定定理的应用，二面角的平面角以及异面直线所成角的求法，考查空间想象能力以及计算能力．