题目内容
9.已知△ABC,AB=4,BC=3,AC=5,现以AB为轴旋转一周,则所得几何体的表面积( )| A. | 24π | B. | 21 π | C. | 33π | D. | 39 π |
分析 易得此几何体为圆锥,圆锥的侧面积=底面周长×母线长÷2,即可求出几何体的表面积.
解答 解:∵在△ABC中,AB=4,BC=3,AC=5,
∴△ABC为直角三角形,
∴底面周长=6π,侧面积=$\frac{1}{2}×$6π×5=15π,
∴几何体的表面积=15π+π•32=24π.
故选:A.
点评 本题考查了圆锥的计算,以及勾股定理的逆定理,利用圆的周长公式和扇形面积公式求解.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
14.若实数k满足0<k<9,则曲线$\frac{{x}^{2}}{25}$-$\frac{{y}^{2}}{9-k}$=1与曲线$\frac{{x}^{2}}{25-k}$-$\frac{{y}^{2}}{9}$=1的( )
| A. | 离心率相等 | B. | 虚半轴长相等 | C. | 实半轴长相等 | D. | 焦距相等 |
19.已知sinα+cosα=$\frac{1}{5}$,则sinα•cosα的值为( )
| A. | $\frac{12}{25}$ | B. | -$\frac{12}{25}$ | C. | -$\frac{7}{5}$ | D. | $\frac{7}{5}$ |
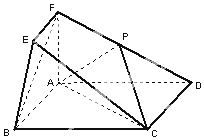 在如图所示的几何体中,四边形ABCD为矩形,平面ABEF⊥平面ABCD,EF∥AB,∠BAF=90°,AD=2,AB=AF=2EF=l,点P在棱DF上.
在如图所示的几何体中,四边形ABCD为矩形,平面ABEF⊥平面ABCD,EF∥AB,∠BAF=90°,AD=2,AB=AF=2EF=l,点P在棱DF上.