题目内容
11.抛物线y=x2-2x-3与坐标轴的交点在同一个圆上,则交点确定的圆的方程为(x-1)2+(y+1)2=5.分析 由已知抛物线方程求出圆心横坐标,设出圆心纵坐标,由圆心到圆上两点的距离等于圆的半径列式求解.
解答 解:抛物线y=x2-2x-3的图象关于x=1对称,与坐标轴的交点为A(-1,0),B(3,0),C(0,-3),
令圆心坐标M(1,b),可得|MA|2=|MC|2=r2,
即4+b2=1+(b+3)2=r2,解得b=-1,r=$\sqrt{5}$.
∴圆的轨迹方程为(x-1)2+(y+1)2=5.
故答案为:(x-1)2+(y+1)2=5.
点评 本题考查抛物线的简单性质,考查数学转化思想方法,是中档题.

练习册系列答案
相关题目
2.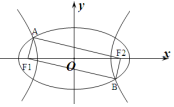 如图F1、F2是椭圆C1:$\frac{{x}^{2}}{4}$+y2=1与双曲线C2的公共焦点,A、B分别是C1、C2在第二、四象限的公共点,若四边形AF1BF2为矩形,则C2的离心率是( )
如图F1、F2是椭圆C1:$\frac{{x}^{2}}{4}$+y2=1与双曲线C2的公共焦点,A、B分别是C1、C2在第二、四象限的公共点,若四边形AF1BF2为矩形,则C2的离心率是( )
 如图F1、F2是椭圆C1:$\frac{{x}^{2}}{4}$+y2=1与双曲线C2的公共焦点,A、B分别是C1、C2在第二、四象限的公共点,若四边形AF1BF2为矩形,则C2的离心率是( )
如图F1、F2是椭圆C1:$\frac{{x}^{2}}{4}$+y2=1与双曲线C2的公共焦点,A、B分别是C1、C2在第二、四象限的公共点,若四边形AF1BF2为矩形,则C2的离心率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{6}}{2}$ |
6.已知f(x)为偶函数,且f(x)=f(x-4),在区间[0,2]上,f(x)=$\left\{\begin{array}{l}{-{x}^{2}-\frac{3}{2}x+5,0≤x≤1}\\{{2}^{x}+{2}^{-x},a<x≤2}\end{array}\right.$,g(x)=($\frac{1}{2}$)|x|+a,若F(x)=f(x)-g(x)恰好有4个零点,则a的取值范围是( )
| A. | (2,$\frac{19}{8}$) | B. | (2,3) | C. | (2,$\frac{19}{8}$] | D. | (2,3] |
3.已知函数f(x)=x3+x-1,则在下列区间中,f(x)一定有零点的是( )
| A. | (-1,0) | B. | (0,1) | C. | (-2,-1) | D. | (1,2) |