题目内容
6.设函数f(x)=alnx-bx2(x>0),若函数y=f(x)在x=1处与直线y=-1相切.(1)求实数a,b的值;
(2)求函数y=f(x)在$[{\frac{1}{e},e}]$上的最小值.
分析 (1)求出函数的导数,通过f(1)=-1,f′(1)=0,求出a,b的值即可;
(2)求出函数f(x)的导数,根据函数的单调性求出f(x)的最小值即可.
解答 解:(1)$f'(x)=\frac{a}{x}-2bx$…(1分),
∵函数y=f(x)在x=1处与直线y=-1相切.
∴$\left\{\begin{array}{l}f'(1)=a-2b=0\\ f(1)=-b=-1\end{array}\right.$…(3分),
解得:a=2,b=1…(4分),
(2)由(1)得,$f(x)=2lnx-{x^2},f'(x)=\frac{2}{x}-2x=\frac{{2({1-{x^2}})}}{x}$.
令f(x)=0,∵x>0,∴x=1…(5分),
当$x∈({\frac{1}{e},1}),f'(x)>0,x∈({1,e}),f'(x)<0$,
∴x=1为函数y=f(x)的极大值点,…(8分),
又$f(1)=-1,f({\frac{1}{e}})=-2-\frac{1}{e^2}<-1$,f(e)=2-e2<-1,
∴f(x)min=f(e)=2-e2.…(10分)
点评 本题考查了函数的单调性、最值问题,考查导数的应用,是一道中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.若实数k满足0<k<9,则曲线$\frac{{x}^{2}}{25}$-$\frac{{y}^{2}}{9-k}$=1与曲线$\frac{{x}^{2}}{25-k}$-$\frac{{y}^{2}}{9}$=1的( )
| A. | 离心率相等 | B. | 虚半轴长相等 | C. | 实半轴长相等 | D. | 焦距相等 |
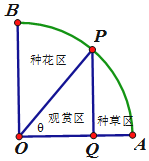 如图,一个圆心角为直角的扇形AOB 花草房,半径为1,点P 是花草房弧上一个动点,不含端点,现打算在扇形BOP 内种花,PQ⊥OA,垂足为Q,PQ 将扇形AOP
如图,一个圆心角为直角的扇形AOB 花草房,半径为1,点P 是花草房弧上一个动点,不含端点,现打算在扇形BOP 内种花,PQ⊥OA,垂足为Q,PQ 将扇形AOP