题目内容
已知一个几何体的三视图及尺寸如图所示,则该几何体的体积为( )


A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:由三视图求面积、体积
专题:计算题,空间位置关系与距离
分析:由已知中的三视图,可得该几何体是由一个三棱柱,挖去一个三棱锥,所得的组合体,进而可得答案.
解答:
解:由已知中的三视图,可得该几何体是:一个三棱柱挖掉一个三棱锥,所得的组合体,
∵三棱柱的体积V=
×12×2=
,
挖去的棱锥体积V′=
×
×12×1=
,
故该几何体的体积为
-
=
.
故选:A.
∵三棱柱的体积V=
| ||
| 4 |
| ||
| 2 |
挖去的棱锥体积V′=
| 1 |
| 3 |
| ||
| 4 |
| ||
| 12 |
故该几何体的体积为
| ||
| 2 |
| ||
| 12 |
5
| ||
| 12 |
故选:A.
点评:本题考查的知识点是由三视图求体积,其中分析出几何体的形状是解答的关键.

练习册系列答案
相关题目
已知椭圆
+
=1上的一点M到焦点F1的距离为2,N是MF1的中点,O为原点,则|ON|等于( )
| x2 |
| 25 |
| y2 |
| 9 |
| A、2 | ||
| B、4 | ||
| C、8 | ||
D、
|
a,b是异面直线,点P∉a∪b,下列命题:
(1)过P可作平面与a,b均平行;
(2)过P可作直线与a,b都相交;
(3)过P可作平面与a,b都垂直;
(4)过P可作直线a,b都垂直,
其中真命题的个数是( )
(1)过P可作平面与a,b均平行;
(2)过P可作直线与a,b都相交;
(3)过P可作平面与a,b都垂直;
(4)过P可作直线a,b都垂直,
其中真命题的个数是( )
| A、1 | B、2 | C、3 | D、4 |
(1)若函数f(x)=2x2-ax-1在(0,1)内存在x0,使得f(x0)=0,求a的取值范围.
(2)方程mx2+2(m+3)x+2m+14=0有两相异实根,一个大于4,一个小于4,求m的取值范围.
(2)方程mx2+2(m+3)x+2m+14=0有两相异实根,一个大于4,一个小于4,求m的取值范围.
已知函数f(x)=-x3+bx2-
b3(b>0),有且仅有两个不同的零点x1,x2,则( )
| 4 |
| 27 |
| A、x1+x2>0,x1x2<0 |
| B、x1+x2>0,x1x2>0 |
| C、x1+x2<0,x1x2<0 |
| D、x1+x2<0,x1x2>0 |
已知a,b,c,d是四条不重合的直线,其中c为a在平面α上的射影,d为b在平面α上的射影,则( )
| A、c∥d⇒a∥b |
| B、a⊥b⇒c⊥d |
| C、a∥b⇒c∥d |
| D、c⊥d⇒a⊥b |
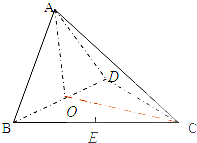 如图,在三棱锥A-BCD中,AO⊥平面BCD;O,E分别是BD,BC的中点,CA=CB=CD=BD=2,AB=AD=
如图,在三棱锥A-BCD中,AO⊥平面BCD;O,E分别是BD,BC的中点,CA=CB=CD=BD=2,AB=AD=