题目内容
设A是椭圆
+
=1(a>b>0)长轴上的一个顶点,若椭圆存在点P,使AP⊥OP,求椭圆离心率e的取值范围.
| x2 |
| a2 |
| y2 |
| b2 |
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:由于∠AP0=90゜,可得点P所在的圆的方程x2+y2-ax=0,与椭圆方程联立可得交点P的横坐标,即a与b的关系,再利用离心率计算公式即可得出.
解答:
解:∵∠AP0=90゜,∴点P在以AO为直径的圆上,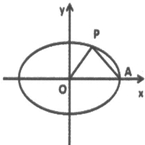
∵O(0,0),A(a,0),
∴以AO为直径的圆方程为x2+y2-ax=0,
联立
消去y,得(b2-a2)x2+a3x-a2b2=0.
设P(m,n),则m+a=-
,ma=
,可得m=
.
∵由图形得0<m<a,∴0<
<a,
即b2<a2-b2,可得a2-c2<c2,得a2<2c2
∴e2>
,∴e>
.
又∵e∈(0,1),
∴椭圆的离心率e的取值范围为(
,1).

∵O(0,0),A(a,0),
∴以AO为直径的圆方程为x2+y2-ax=0,
联立
|
消去y,得(b2-a2)x2+a3x-a2b2=0.
设P(m,n),则m+a=-
| a3 |
| b2-a2 |
| -a2b2 |
| b2-a2 |
| ab2 |
| a2-b2 |
∵由图形得0<m<a,∴0<
| ab2 |
| a2-b2 |
即b2<a2-b2,可得a2-c2<c2,得a2<2c2
∴e2>
| 1 |
| 2 |
| ||
| 2 |
又∵e∈(0,1),
∴椭圆的离心率e的取值范围为(
| ||
| 2 |
点评:本题考查了圆与椭圆相交问题转化为方程联立可得根与系数的关系、椭圆的离心率范围性质,考查了推理能力与计算能力,属于难题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
椭圆
+
=1(a>b>0)的两个焦点是F1、F2,以|F1F2|为斜边作等腰直角三角形,若椭圆恰好平分三角形的另两边,则椭圆的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
已知一个几何体的三视图及尺寸如图所示,则该几何体的体积为( )


A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若点M(x,y)为平面区域
上的一个动点,则x+2y的最大值是( )
|
| A、-1 | ||
B、-
| ||
| C、0 | ||
| D、1 |
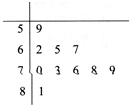 已知某单位由50名职工,将全体职工随机按1-50编号,并且按编号顺序平均分成10组,先要从中抽取10名职工,各组内抽取的编号依次增加5进行系统抽样.
已知某单位由50名职工,将全体职工随机按1-50编号,并且按编号顺序平均分成10组,先要从中抽取10名职工,各组内抽取的编号依次增加5进行系统抽样.