题目内容
已知a，b，c，d是四条不重合的直线，其中c为a在平面α上的射影，d为b在平面α上的射影，则（ ）
| A、c∥d⇒a∥b |
| B、a⊥b⇒c⊥d |
| C、a∥b⇒c∥d |
| D、c⊥d⇒a⊥b |
考点：空间中直线与直线之间的位置关系
专题：空间位置关系与距离
分析：以正方体为载体，利用空间中线线、线面、面面间的位置关系求解．
解答：
解：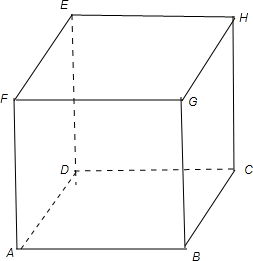
把a，b，c，d这四条不重合的直线都放在正方体ABCD-EFGH中．
对于A：取a=GH，d=BC，b=FD，
满足要求a∥d，但推不出a∥b，所以A为假命题；
对于B：取a=BH，b=FD，C=BC，d=AD，
满足要求a⊥b，但推不出c⊥d，所以B为假命题；
对于C：因为斜线平行时，
对应的射影要么平行，要么重合，要么为两个点，
而题中交代a，b，c，d是四条不重合的直线，
故射影平行，所以C为真命题；
对于D：取c=BC，d=AB，b=FB，a=BH，
此时a，b所成角为60°，满足要求c⊥d，
但推不出a⊥b，所以D为假命题．
故选：C．
把a，b，c，d这四条不重合的直线都放在正方体ABCD-EFGH中．对于A：取a=GH，d=BC，b=FD，
满足要求a∥d，但推不出a∥b，所以A为假命题；
对于B：取a=BH，b=FD，C=BC，d=AD，
满足要求a⊥b，但推不出c⊥d，所以B为假命题；
对于C：因为斜线平行时，
对应的射影要么平行，要么重合，要么为两个点，
而题中交代a，b，c，d是四条不重合的直线，
故射影平行，所以C为真命题；
对于D：取c=BC，d=AB，b=FB，a=BH，
此时a，b所成角为60°，满足要求c⊥d，
但推不出a⊥b，所以D为假命题．
故选：C．
点评：本题考查命题真假的判断，是基础题，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
相关题目
已知一个几何体的三视图及尺寸如图所示，则该几何体的体积为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若点M（x，y）为平面区域
上的一个动点，则x+2y的最大值是（ ）
|
| A、-1 | ||
B、-
| ||
| C、0 | ||
| D、1 |
已知函数f（x）=ln（ax）-
（a≠0）．
（1）求此函数的单调区间及最值；
（2）当a=1时，是否存在过点（-1，1）的直线与函数y=f（x）的图象相切？若存在，有多少条？若不存在，说明理由．
| x-a |
| x |
（1）求此函数的单调区间及最值；
（2）当a=1时，是否存在过点（-1，1）的直线与函数y=f（x）的图象相切？若存在，有多少条？若不存在，说明理由．
已知函数g（x）是R上的奇函数，且当x＜0时g（x）=-ln（1-x），设函数f（x）=
，若f（2-x2）＞f（x），则实数x的取值范围是（ ）
|
| A、（-∞，1）∪（2，+∞） |
| B、（-∞，-2）∪（1，+∞） |
| C、（1，2） |
| D、（-2，1） |