Question

已知椭圆C：

x2

a2

+

y2

b2

=1(a＞b＞0)过点A（-1，1），离心率为

6

3

（I）求椭圆C的方程
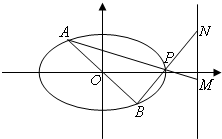
（II）设点B是点A关于原点的对称点，P是椭圆C上的动点（不同于A，B），直线AP，BP分别与直线x=3交于点M，N，问是否存在点P使得△PAB和△PMN的面积相等，若存在，求出点P的坐标，若不存在请说明理由．

Answer 1

考点：直线与圆锥曲线的综合问题

专题：圆锥曲线中的最值与范围问题

分析：（Ⅰ）由已知条件推导出

1 a2 + 1 b2 =1 a2=b2+c2 c a = 6 3

，由此能求出椭圆C的方程．
（Ⅱ）B点坐标为（1，-1），假设存在这样的点P（x₀，y₀），设出直线AP的方程和直线BP的方程，由直线AP，BP分别与直线x=3交于点M，N，得△PMN的面积=

|x0+y0|(3-x0)2

|x02-1|

，△PAB的面积=|x₀+y₀|，由此能确定存在点P使得△PAB和△△PMN的面积相等，并能求出点P坐标．

解答： 解：（Ⅰ）∵椭圆C：

x2

a2

+

y2

b2

=1(a＞b＞0)过点A（-1，1），离心率为

6

3

，
∴

1 a2 + 1 b2 =1 a2=b2+c2 c a = 6 3

，解得a²=4，b²=

4

3

，
∴椭圆C的方程为

x2

4

+

3y2

4

=1．
（Ⅱ）如图，B点坐标为（1，-1），假设存在这样的点P（x₀，y₀），
则直线AP的方程为y-1=

y0-1

x0+1

(x-1)，
直线BP的方程为y+1=

y0+1

x0-1

(x+1)，
∵直线AP，BP分别与直线x=3交于点M，N，
∴令x=3，得yM=

4y0+x0-3

x0+1

，yN=

2y0-x0+3

x0-1

，
∴△PMN的面积S△PMN=

1

2

|y_M-y_N|（3-x₀）
=

|x0+y0|(3-x0)2

|x02-1|

，
又∵AB=2

2

，直线AB的方程为x+y=0，
∴点P到直线AB的距离d=

|x0+y0|

2

，
∴△PAB的面积S_△PAB=

1

2

AB•d=|x₀+y₀|，
∵点P不同于A，B，∴|x₀+y₀|≠0，
∴（3-x₀）²=|x02-1|，
解得x0=

5

3

，从而y₀=±

33

9

，
∴存在点P使得△PAB和△△PMN的面积相等，点P坐标为（

5

3

，±

33

9

）．

点评：本题考查椭圆方程的求法，考查满足条件的点是否存在的确定，综合性强，难度大，具有一定的确定