题目内容
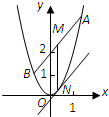
已知抛物线C的顶点在原点，经过点A（1，2），其焦点F在y轴上，直线y=kx+2交抛物线C于A，B两点，M是线段AB的中点，过M作x轴的垂线交抛物线C于点N．
（Ⅰ）求抛物线C的方程；
（Ⅱ）证明：抛物线C在点N处的切线与AB平行．
（Ⅰ）求抛物线C的方程；
（Ⅱ）证明：抛物线C在点N处的切线与AB平行．
考点：直线与圆锥曲线的综合问题
专题：综合题,圆锥曲线的定义、性质与方程
分析：（Ⅰ）设抛物线C的方程为y=ax2，利用点A（1，2）在抛物线C上，即可求抛物线C的方程；
（Ⅱ）把y=kx+2代入y=2x2，利用韦达定理，确定N的坐标，从而可得抛物线在点N处的切线l的方程，进而可证明切线l的与k相等，即可得到结论．
（Ⅱ）把y=kx+2代入y=2x2，利用韦达定理，确定N的坐标，从而可得抛物线在点N处的切线l的方程，进而可证明切线l的与k相等，即可得到结论．
解答：
解：依题意，设抛物线C的方程为y=ax2，
（Ⅰ）∵点A（1，2）在抛物线C上，∴a=1．
∴抛物线C的方程为y=2x2．…（4分）
（Ⅱ）如图，设A（x1，2x12），B（x2，2x22），
把y=kx+2代入y=2x2得：2x2-kx-2=0，
由韦达定理得：x1+x2=
，x1x2=-1，∴xN=xM=
=
，
即N点的坐标为（
，
）．…（8分）
设抛物线在点N处的切线l的方程为y-
=m（x-
），
将y=2x2代入上式得：2x2-mx+
-
=0，
∵直线l与抛物线C相切，所以△=m2-8（
-
）=m2-2mk+k2=（m-k）2=0，
∴m=k，即l∥AB．…（12分）
解：依题意，设抛物线C的方程为y=ax2，（Ⅰ）∵点A（1，2）在抛物线C上，∴a=1．
∴抛物线C的方程为y=2x2．…（4分）
（Ⅱ）如图，设A（x1，2x12），B（x2，2x22），
把y=kx+2代入y=2x2得：2x2-kx-2=0，
由韦达定理得：x1+x2=
| k |
| 2 |
| x1+x2 |
| 2 |
| k |
| 4 |
即N点的坐标为（
| k |
| 4 |
| k2 |
| 8 |
设抛物线在点N处的切线l的方程为y-
| k2 |
| 8 |
| k |
| 4 |
将y=2x2代入上式得：2x2-mx+
| mk |
| 4 |
| k2 |
| 8 |
∵直线l与抛物线C相切，所以△=m2-8（
| mk |
| 4 |
| k2 |
| 8 |
∴m=k，即l∥AB．…（12分）
点评：本题考查抛物线的方程，考查直线与抛物线的位置关系，考查韦达定理的运用，考查抛物线的切线，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
已知i为虚数单位，则复数
的共轭复数是（ ）
| 2i |
| 1+i |
| A、1+i | B、1-i |
| C、-1+i | D、-1-i |
已知函数f（x）=x2+bx（b∈R），则下列结论正确的是（ ）
| A、?b∈R，f（x）在（0，+∞）上是增函数 |
| B、?b∈R，f（x）在（0，+∞）上是减函数 |
| C、?b∈R，f（x）为奇函数 |
| D、?b∈R，f（x）为偶函数 |
已知椭圆
已知A，B分别是椭圆