题目内容
给出如下四个命题:
①若“p且q”为假命题,则p、q均为假命题
②命题“若xy=0,则x=0或y=0”的否命题为“若xy≠0,则x≠0且y≠0”
③“任意x∈R,x2+1≥1”的否定是“存在x∈R,x2+1≤1”
④在△ABC中,“A>B”是“sinA>sinB”的充要条件
其中正确的命题的个数是( )
①若“p且q”为假命题,则p、q均为假命题
②命题“若xy=0,则x=0或y=0”的否命题为“若xy≠0,则x≠0且y≠0”
③“任意x∈R,x2+1≥1”的否定是“存在x∈R,x2+1≤1”
④在△ABC中,“A>B”是“sinA>sinB”的充要条件
其中正确的命题的个数是( )
| A、4 | B、3 | C、2 | D、1 |
考点:命题的真假判断与应用
专题:简易逻辑,推理和证明
分析:对于①,根据命题的真值表,若“p且q”为假命题,则两个命题p、q至少一个为假,未必都假,所以是不正确的.
对于②,根据否命题的写法,否定条件,否定结论,②是正确的.
对于③,根据全称命题的否定形式,“任意x∈R,x2+1≥1”的否定应该是“存在x∈R,x2+1<1”.
对于④,根据正弦定理,以及大角对大边原理,④是正确的.
对于②,根据否命题的写法,否定条件,否定结论,②是正确的.
对于③,根据全称命题的否定形式,“任意x∈R,x2+1≥1”的否定应该是“存在x∈R,x2+1<1”.
对于④,根据正弦定理,以及大角对大边原理,④是正确的.
解答:
解:对于①,因为“p且q”为假命题,根据命题的真值表,所以p与q至少一个不正确,未必都不正确,
故①错误.
对于②,命题“若xy=0,则x=0或y=0”的否命题为“若xy≠0,则x≠0且y≠0”正确,即②正确.
对于③,根据全称命题的否定形式,“任意x∈R,x2+1≥1”的否定是“存在x∈R,x2+1<1”,故③错误.
对于④,在三角形ABC中,根据正弦定理和三角形的大边对大角原理,“A>B”?a>b?sinA>sinB,故④正确.
故选:C.
故①错误.
对于②,命题“若xy=0,则x=0或y=0”的否命题为“若xy≠0,则x≠0且y≠0”正确,即②正确.
对于③,根据全称命题的否定形式,“任意x∈R,x2+1≥1”的否定是“存在x∈R,x2+1<1”,故③错误.
对于④,在三角形ABC中,根据正弦定理和三角形的大边对大角原理,“A>B”?a>b?sinA>sinB,故④正确.
故选:C.
点评:本题考查了命题的真值表,否命题,真命题的书写形式,对于④,是个简单题目,但容易出错.

练习册系列答案
相关题目
已知i为虚数单位,则复数
的共轭复数是( )
| 2i |
| 1+i |
| A、1+i | B、1-i |
| C、-1+i | D、-1-i |
已知变量x,y满足约束条件
,则目标函数z=6x-2y的最小值为( )
|
| A、32 | B、4 | C、8 | D、2 |
运行如图所示的程序框图,则输出的结果S为( )


| A、1007 | B、1008 |
| C、2013 | D、2014 |
下面几个命题中,假命题是( )
| A、“若a≤b,则2a≤2b-1”的否命题 |
| B、“?a∈(0,+∞),函数y=ax在定义域内单调递增”的否定 |
| C、“π是函数y=sinx的一个周期”或“2π是函数y=sin2x的一个周期” |
| D、“x2+y2=0”是“xy=0”的必要条件. |
已知函数f(x)=x2+bx(b∈R),则下列结论正确的是( )
| A、?b∈R,f(x)在(0,+∞)上是增函数 |
| B、?b∈R,f(x)在(0,+∞)上是减函数 |
| C、?b∈R,f(x)为奇函数 |
| D、?b∈R,f(x)为偶函数 |
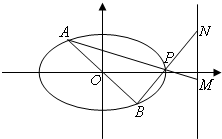 已知椭圆
已知椭圆