题目内容
将曲线C1:(x-4)2+y2=4所有点的横坐标不变,纵坐标变为原来的
得到曲线C2,将曲线C2向左(x轴负方向)平移4个单位,得到曲线C3.
(Ⅰ)求曲线C3的方程;
(Ⅱ)垂直于x轴的直线l与曲线C3相交于C、D两点(C、D可以重合),已知A(-2,0),B(2,0),直线AC、BD相交于点P,求P点的轨迹方程.
| 1 |
| 2 |
(Ⅰ)求曲线C3的方程;
(Ⅱ)垂直于x轴的直线l与曲线C3相交于C、D两点(C、D可以重合),已知A(-2,0),B(2,0),直线AC、BD相交于点P,求P点的轨迹方程.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)由题设条件推导出C2:(x-4)2+(2x)2=1,再由平移的计算能求出曲线C3的方程.
(Ⅱ)若C、D重合,则P(-2,0)或P(2,0),若C、D不重合,设C(x0,y0)(-2<x0<2),则D(x0,-y0),由此能求出P点的轨迹方程.
(Ⅱ)若C、D重合,则P(-2,0)或P(2,0),若C、D不重合,设C(x0,y0)(-2<x0<2),则D(x0,-y0),由此能求出P点的轨迹方程.
解答:
解:(Ⅰ) 将C1:(x-4)2+y2=1所有点的横坐标不变,
纵坐标变为原来的
得到的曲线方程为(x-4)2+(2x)2=1,
即C2:(x-4)2+(2x)2=1,
再将C2:(x-4)2+(2x)2=1向左平移4个单位得到的曲线方程为x2+(2x)2=4,
即曲线C3的方程为
+y2=1.…(6分)
(Ⅱ)若C、D重合,则P(-2,0)或P(2,0),
若C、D不重合,设C(x0,y0)(-2<x0<2),则D(x0,-y0),
∴直线AC的方程为y=
(x+2),
直线BD的直线方程为y=-
(x-2),
∴y2=-
(x+2)(x-2),
即y2=-
(x2-4).(1)
∵C、D点在C3:
+y2=1上,
∴
+
=1,
∴-
=
,(2)
把(2)代入(1)化简得
-y2=1.
综上所述,P点的轨迹方程为
-y2=1.…(12分)
纵坐标变为原来的
| 1 |
| 2 |
即C2:(x-4)2+(2x)2=1,
再将C2:(x-4)2+(2x)2=1向左平移4个单位得到的曲线方程为x2+(2x)2=4,
即曲线C3的方程为
| x2 |
| 4 |
(Ⅱ)若C、D重合,则P(-2,0)或P(2,0),
若C、D不重合,设C(x0,y0)(-2<x0<2),则D(x0,-y0),
∴直线AC的方程为y=
| y0 |
| x0+2 |
直线BD的直线方程为y=-
| y0 |
| x0-2 |
∴y2=-
| ||
| (x0+2)(x0-2) |
即y2=-
| ||
|
∵C、D点在C3:
| x2 |
| 4 |
∴
| ||
| 4 |
| y | 2 0 |
∴-
| ||
|
| 1 |
| 4 |
把(2)代入(1)化简得
| x2 |
| 4 |
综上所述,P点的轨迹方程为
| x2 |
| 4 |
点评:本题考查曲线方程的求法,考查点的轨迹方程的求法,解题时要注意伸缩变换和平移变换的合理运用.

练习册系列答案
相关题目
已知变量x,y满足约束条件
,则目标函数z=6x-2y的最小值为( )
|
| A、32 | B、4 | C、8 | D、2 |
下面几个命题中,假命题是( )
| A、“若a≤b,则2a≤2b-1”的否命题 |
| B、“?a∈(0,+∞),函数y=ax在定义域内单调递增”的否定 |
| C、“π是函数y=sinx的一个周期”或“2π是函数y=sin2x的一个周期” |
| D、“x2+y2=0”是“xy=0”的必要条件. |
已知函数f(x)=x2+bx(b∈R),则下列结论正确的是( )
| A、?b∈R,f(x)在(0,+∞)上是增函数 |
| B、?b∈R,f(x)在(0,+∞)上是减函数 |
| C、?b∈R,f(x)为奇函数 |
| D、?b∈R,f(x)为偶函数 |
 如图,椭圆C1:
如图,椭圆C1: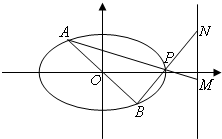 已知椭圆
已知椭圆