题目内容
已知函数g(x)是R上的奇函数,且当x<0时,g(x)=-ln(1-x),设函数f(x)=
,若f(x2-x)<f(6-2x),则实数x的取值范围是( )
|
| A、(-∞,-3)∪(2,+∞) |
| B、(-∞,-2)∪(3,+∞) |
| C、(-2,3) |
| D、(-3,2) |
考点:分段函数的应用
专题:计算题,函数的性质及应用
分析:由函数g(x)是R上的奇函数,且当x<0时,g(x)=-ln(1-x)可求得当x>0时,g(x)=ln(1+x),从而化简f(x)=
,由函数的单调性求解.
|
解答:
解:∵函数g(x)是R上的奇函数,且当x<0时,g(x)=-ln(1-x),
∴当x>0时,
g(x)=-g(-x)=ln(1+x),
故f(x)=
,
易知f(x)在R上是增函数,
故由f(x2-x)<f(6-2x)得,
x2-x<6-2x,
即x2+x-6<0,
解得,-3<x<2,
故选D.
∴当x>0时,
g(x)=-g(-x)=ln(1+x),
故f(x)=
|
易知f(x)在R上是增函数,
故由f(x2-x)<f(6-2x)得,
x2-x<6-2x,
即x2+x-6<0,
解得,-3<x<2,
故选D.
点评:本题考查了分段函数的应用及函数的奇偶性的应用,属于中档题.

练习册系列答案
相关题目
已知A,B,C三点共线,O为直径AB外的任一点,满足
=x
+y
,则x2+y的最小值等于( )
| OC |
| OA |
| OB |
A、
| ||
| B、1 | ||
C、
| ||
D、
|
函数f(x)=ax2+2(a-3)x+1在区间[-3,+∞)上递减,则实数a的取值范围是( )
| A、(-∞,0) | ||
B、[-
| ||
C、[-
| ||
| D、(0,+∞) |
平面向量
=(-1,1),
=(1,2),且
•
=3,则
•
=( )
| AB |
| n |
| n |
| AC |
| n |
| BC |
| A、-2 | B、2 | C、3 | D、4 |
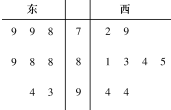 某城市要建成宜商、宜居的国际化新城,该城市的东城区、西城区分别引进8个厂家,现对两个区域的16个厂家进行评估,综合得分情况如茎叶图所示.
某城市要建成宜商、宜居的国际化新城,该城市的东城区、西城区分别引进8个厂家,现对两个区域的16个厂家进行评估,综合得分情况如茎叶图所示.