题目内容
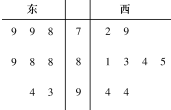 某城市要建成宜商、宜居的国际化新城,该城市的东城区、西城区分别引进8个厂家,现对两个区域的16个厂家进行评估,综合得分情况如茎叶图所示.
某城市要建成宜商、宜居的国际化新城,该城市的东城区、西城区分别引进8个厂家,现对两个区域的16个厂家进行评估,综合得分情况如茎叶图所示.(1)根据茎叶图判断哪个区域厂家的平均分较高;
(2)规定综合得分85分以上(含85分)为优秀厂家,若从该两个区域各选一个优秀厂家,求得分差距不超过5分的概率.
考点:列举法计算基本事件数及事件发生的概率,茎叶图
专题:概率与统计
分析:(Ⅰ)根据茎叶图求出东城区与西城区的平均分即可得出结论;
(Ⅱ)求出从两个区域各选一个优秀厂家的所有基本事件数,再求出满足得分差距不超过5的事件数,即可求出概率.
(Ⅱ)求出从两个区域各选一个优秀厂家的所有基本事件数,再求出满足得分差距不超过5的事件数,即可求出概率.
解答:
解:(Ⅰ)根据茎叶图知,东城区的平均分为
=
(780+790+790+88+88+89+93+94)=86,
西城区的平均分为
=
(72+79+81+83+84+85+94+94)=84,
∴东城区的平均分较高;
(Ⅱ)从两个区域各选一个优秀厂家,
所有的基本事件数为5×3=15种,
满足得分差距不超过5的事件(88,85)(88,85)(89,85)(89,94)(89,94)(93,94)(93,94)(94,94)(94,94)共9种,
∴满足条件的概率为P=
=
.
. |
| x东 |
| 1 |
| 8 |
西城区的平均分为
. |
| x西 |
| 1 |
| 8 |
∴东城区的平均分较高;
(Ⅱ)从两个区域各选一个优秀厂家,
所有的基本事件数为5×3=15种,
满足得分差距不超过5的事件(88,85)(88,85)(89,85)(89,94)(89,94)(93,94)(93,94)(94,94)(94,94)共9种,
∴满足条件的概率为P=
| 9 |
| 15 |
| 3 |
| 5 |
点评:本题通过茎叶图考查了平均数以及古典概型的概率问题,解题时应列出基本事件,属于基础题

练习册系列答案
 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
已知函数f(x)满足f(x+1)=
,且当x∈(0,1]时,f(x)=x,g(x)=m(x+3),若方程f(x)=g(x)在区间(-1,1]上有两个不同的实根,则实数m的取值范围是( )
| 1 |
| f(x)+1 |
A、(0,
| ||
B、(0,
| ||
C、(
| ||
D、(
|
已知函数g(x)是R上的奇函数,且当x<0时,g(x)=-ln(1-x),设函数f(x)=
,若f(x2-x)<f(6-2x),则实数x的取值范围是( )
|
| A、(-∞,-3)∪(2,+∞) |
| B、(-∞,-2)∪(3,+∞) |
| C、(-2,3) |
| D、(-3,2) |
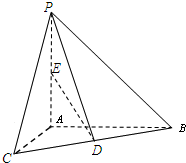 如图,已知PA⊥平面ABC,AC⊥AB,AP=BC=2,∠CBA=30°,D、E分别是BC、AP的中点.求异面直线AC与ED所成的角的大小为
如图,已知PA⊥平面ABC,AC⊥AB,AP=BC=2,∠CBA=30°,D、E分别是BC、AP的中点.求异面直线AC与ED所成的角的大小为