题目内容
函数f(x)=logax(a>0,a≠1)在[2,3]中最大值比最小值大1,则a的值为 .
考点:对数函数的图像与性质
专题:函数的性质及应用
分析:分当a>1时和当0<a<1时两种情况,分别利用对数函数的定义域和单调性求得a的值,从而得出结论.
解答:
解:当a>1时,函数y=logax(a>0且a≠1)在∈[2,3]上是增函数,
根据题意可得 loga3-loga2=1,求得 a=
.
当0<a<1时,函数y=logax(a>0且a≠1)在∈[2,3]上是减函数,
根据题意可得loga2-loga3=1,求得 a=
.
综上可得,a=
,或a=
,
故答案为:a=
或a=
,
根据题意可得 loga3-loga2=1,求得 a=
| 3 |
| 2 |
当0<a<1时,函数y=logax(a>0且a≠1)在∈[2,3]上是减函数,
根据题意可得loga2-loga3=1,求得 a=
| 2 |
| 3 |
综上可得,a=
| 3 |
| 2 |
| 2 |
| 3 |
故答案为:a=
| 3 |
| 2 |
| 2 |
| 3 |
点评:本题考查了对数函数的单调性,考查了分类讨论的数学思想方法,训练了对数方程的解法,是基础题.

练习册系列答案
相关题目
已知函数g(x)是R上的奇函数,且当x<0时,g(x)=-ln(1-x),设函数f(x)=
,若f(x2-x)<f(6-2x),则实数x的取值范围是( )
|
| A、(-∞,-3)∪(2,+∞) |
| B、(-∞,-2)∪(3,+∞) |
| C、(-2,3) |
| D、(-3,2) |
函数y=Asin(ωx+φ)+k(A>0,ω>0,|φ|≤
,x∈R)的部分图象如图所示,则该函数表达式为( )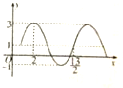
| π |
| 6 |

A、y=2sin(
| ||||
B、y=2sin(
| ||||
C、y=2sin(
| ||||
D、y=2sin(
|
函数y=
的定义域为( )
| 1-lnx |
| A、(0,e] |
| B、(-∞,e] |
| C、(0,10] |
| D、(-∞,10] |
 如图,直线x=±π,y=±1围成的矩形区域内有一段余弦曲线y=-cosx,任意地向矩形投掷飞镖,则飞镖落入阴影区域的概率是
如图,直线x=±π,y=±1围成的矩形区域内有一段余弦曲线y=-cosx,任意地向矩形投掷飞镖,则飞镖落入阴影区域的概率是