题目内容
在一次自主招生选拔考核中,每个候选人都需要进行四轮考核,每轮设有一个问题,能正确回答者进入下一轮考核,否则被淘汰,已知某候选人能正确回答第一,二,三,四轮问题的概率分别为
,
,
,
,且各轮问题能否正确回答互不影响.
(I)求该选手进入第三轮才被淘汰的概率;
(Ⅱ)该选手在选拔过程中回答问题的个数记为X,求随机变量X的分布列和期望.
| 5 |
| 6 |
| 4 |
| 5 |
| 3 |
| 4 |
| 1 |
| 3 |
(I)求该选手进入第三轮才被淘汰的概率;
(Ⅱ)该选手在选拔过程中回答问题的个数记为X,求随机变量X的分布列和期望.
考点:离散型随机变量的期望与方差,相互独立事件的概率乘法公式
专题:概率与统计
分析:(Ⅰ)设事件Ai(i=1,2,3,4)表示“该选手能正确回答第i轮问题”,由已知P(A1)=
,P(A2)=
,P(A3)=
,P(A4)=
,设事件B表示“该选手进入第三轮被淘汰”,则P(B)=P(A1A2
),由此能求出结果.
(2)由已知得X=1,2,3,4,分别求出相应的概率,由此能求出随机变量X的分布列和期望.
| 5 |
| 6 |
| 4 |
| 5 |
| 3 |
| 4 |
| 1 |
| 3 |
. |
| A3 |
(2)由已知得X=1,2,3,4,分别求出相应的概率,由此能求出随机变量X的分布列和期望.
解答:
解:(Ⅰ)设事件Ai(i=1,2,3,4)表示“该选手能正确回答第i轮问题”.
由已知P(A1)=
,P(A2)=
,P(A3)=
,P(A4)=
,…(4分)
设事件B表示“该选手进入第三轮被淘汰”,
则P(B)=P(A1A2
)=
×
×(1-
)=
.…(6分)
(2)由已知得X=1,2,3,4,
P(X=1)=
,
P(X=2)=
×(1-
)=
,
P(X=3)=
×
×(1-
)=
,
P(X=4)=
×
×
=
,
∴X的分布列为:
EX=1×
+2×
+3×
+4×
=3.
由已知P(A1)=
| 5 |
| 6 |
| 4 |
| 5 |
| 3 |
| 4 |
| 1 |
| 3 |
设事件B表示“该选手进入第三轮被淘汰”,
则P(B)=P(A1A2
. |
| A3 |
| 5 |
| 6 |
| 4 |
| 5 |
| 3 |
| 4 |
| 1 |
| 6 |
(2)由已知得X=1,2,3,4,
P(X=1)=
| 1 |
| 6 |
P(X=2)=
| 5 |
| 6 |
| 4 |
| 5 |
| 1 |
| 6 |
P(X=3)=
| 5 |
| 6 |
| 4 |
| 5 |
| 3 |
| 4 |
| 1 |
| 6 |
P(X=4)=
| 5 |
| 6 |
| 4 |
| 5 |
| 3 |
| 4 |
| 1 |
| 2 |
∴X的分布列为:
| X | 1 | 2 | 3 | 4 | ||||||||
| P |
|
|
|
|
| 1 |
| 6 |
| 1 |
| 6 |
| 1 |
| 6 |
| 1 |
| 2 |
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题.

练习册系列答案
相关题目
已知函数f(x)=x2+mx-1,若对于任意x∈[m,m+1],都有f(x)<0成立,则实数m的取值范围是( )
| A、(0,1) | ||||
B、(0,
| ||||
| C、(-1,0) | ||||
D、(-
|
已知函数f(x)满足f(x+1)=
,且当x∈(0,1]时,f(x)=x,g(x)=m(x+3),若方程f(x)=g(x)在区间(-1,1]上有两个不同的实根,则实数m的取值范围是( )
| 1 |
| f(x)+1 |
A、(0,
| ||
B、(0,
| ||
C、(
| ||
D、(
|
已知函数g(x)是R上的奇函数,且当x<0时,g(x)=-ln(1-x),设函数f(x)=
,若f(x2-x)<f(6-2x),则实数x的取值范围是( )
|
| A、(-∞,-3)∪(2,+∞) |
| B、(-∞,-2)∪(3,+∞) |
| C、(-2,3) |
| D、(-3,2) |
设f(x)=
,则f[f(ln2+1)]=( )
|
| A、log717 |
| B、2 |
| C、7 |
| D、log7(8e2+1) |
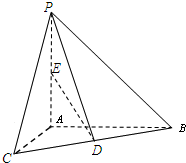 如图,已知PA⊥平面ABC,AC⊥AB,AP=BC=2,∠CBA=30°,D、E分别是BC、AP的中点.求异面直线AC与ED所成的角的大小为
如图,已知PA⊥平面ABC,AC⊥AB,AP=BC=2,∠CBA=30°,D、E分别是BC、AP的中点.求异面直线AC与ED所成的角的大小为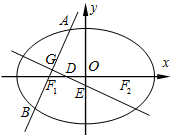 如图,已知椭圆C:
如图,已知椭圆C: