题目内容
在△ABC中,a,b,c分别为角A,B,C的对边,cosA=cos2A+
.
(1)求角A;
(2)若a=
,b+c=3,求b的值.
| 1 |
| 4 |
(1)求角A;
(2)若a=
| 3 |
考点:余弦定理的应用
专题:解三角形
分析:(1)由已知可解得cosA=
,又由00<A<1800从而可得A的值.
(2)由余弦定理a2=b2+c2-2bccosA得bc=2,有由b+c=3,bc=2从而可解得b的值.
| 1 |
| 2 |
(2)由余弦定理a2=b2+c2-2bccosA得bc=2,有由b+c=3,bc=2从而可解得b的值.
解答:
解:(1)由已知,4cos2A-4cosA+1=0,
即(2cosA-1)2=0…(2分)
∴cosA=
…(4分)
又∵00<A<1800…(5分)
∴A=60°…(6分)
(2)由余弦定理a2=b2+c2-2bccosA得:
a2=(b+c)2-2bc-2bccosA,
故3=9-2bc-2bc×
…(9分)
∴bc=2;…(10分)
由b+c=3,bc=2解得,b=1,或b=2.…(12分)
即(2cosA-1)2=0…(2分)
∴cosA=
| 1 |
| 2 |
又∵00<A<1800…(5分)
∴A=60°…(6分)
(2)由余弦定理a2=b2+c2-2bccosA得:
a2=(b+c)2-2bc-2bccosA,
故3=9-2bc-2bc×
| 1 |
| 2 |
∴bc=2;…(10分)
由b+c=3,bc=2解得,b=1,或b=2.…(12分)
点评:本题主要考察了余弦定理的综合应用,属于基本知识的考察.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
已知函数g(x)是R上的奇函数,且当x<0时,g(x)=-ln(1-x),设函数f(x)=
,若f(x2-x)<f(6-2x),则实数x的取值范围是( )
|
| A、(-∞,-3)∪(2,+∞) |
| B、(-∞,-2)∪(3,+∞) |
| C、(-2,3) |
| D、(-3,2) |
设f(x)=
,则f[f(ln2+1)]=( )
|
| A、log717 |
| B、2 |
| C、7 |
| D、log7(8e2+1) |
若直线l:y=-
+m与曲线C:y=
有且仅有三个交点,则m的取值范围是( )
| x |
| 2 |
| 1 |
| 2 |
| |4-x2| |
A、(
| ||||
B、(1,
| ||||
C、(1,
| ||||
D、(2,
|
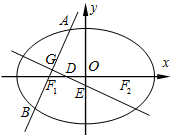 如图,已知椭圆C:
如图,已知椭圆C: