题目内容
平面向量
=(-1,1),
=(1,2),且
•
=3,则
•
=( )
| AB |
| n |
| n |
| AC |
| n |
| BC |
| A、-2 | B、2 | C、3 | D、4 |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:由于
•
=
•(
-
)=
•
-
•
,结合题意利用两个向量的数量积公式,求得
•
的值.
| n |
| AB |
| n |
| AC |
| BC |
| n |
| AC |
| n |
| BC |
| n |
| BC |
解答:
解:由于
•
=
•(
-
)=
•
-
•
,∴由题意可得(1,2)•(-1,1)=3-
•
,
即 1=3-
•
,求得
•
=2,
故选:B.
| n |
| AB |
| n |
| AC |
| BC |
| n |
| AC |
| n |
| BC |
| n |
| BC |
即 1=3-
| n |
| BC |
| n |
| BC |
故选:B.
点评:本题主要考查两个向量的加减法的法则,以及其几何意义,两个向量的数量积公式,两个向量坐标形式的运算,属于基础题.

练习册系列答案
相关题目
已知函数g(x)是R上的奇函数,且当x<0时,g(x)=-ln(1-x),设函数f(x)=
,若f(x2-x)<f(6-2x),则实数x的取值范围是( )
|
| A、(-∞,-3)∪(2,+∞) |
| B、(-∞,-2)∪(3,+∞) |
| C、(-2,3) |
| D、(-3,2) |
设f(x)=
,则f[f(ln2+1)]=( )
|
| A、log717 |
| B、2 |
| C、7 |
| D、log7(8e2+1) |
若直线l:y=-
+m与曲线C:y=
有且仅有三个交点,则m的取值范围是( )
| x |
| 2 |
| 1 |
| 2 |
| |4-x2| |
A、(
| ||||
B、(1,
| ||||
C、(1,
| ||||
D、(2,
|
函数y=Asin(ωx+φ)+k(A>0,ω>0,|φ|≤
,x∈R)的部分图象如图所示,则该函数表达式为( )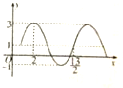
| π |
| 6 |

A、y=2sin(
| ||||
B、y=2sin(
| ||||
C、y=2sin(
| ||||
D、y=2sin(
|
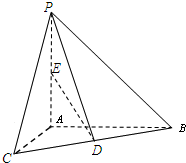 如图,已知PA⊥平面ABC,AC⊥AB,AP=BC=2,∠CBA=30°,D、E分别是BC、AP的中点.求异面直线AC与ED所成的角的大小为
如图,已知PA⊥平面ABC,AC⊥AB,AP=BC=2,∠CBA=30°,D、E分别是BC、AP的中点.求异面直线AC与ED所成的角的大小为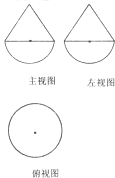 已知一个几何体是由上、下两部分构成的组合体,其三视图如图,若图中圆的半径为l,等腰三角形的腰长为
已知一个几何体是由上、下两部分构成的组合体,其三视图如图,若图中圆的半径为l,等腰三角形的腰长为