题目内容
2.过抛物线y2=2px(p>0)的焦点F,且倾斜角为$\frac{π}{4}$的直线与抛物线交于A,B两点,若弦AB的垂直平分线经过点(0,2),则p等于( )| A. | $\frac{2}{5}$ | B. | $\frac{2}{3}$ | C. | $\frac{4}{5}$ | D. | $\frac{4}{3}$ |
分析 可以求出抛物线的焦点坐标,从而可以写出弦AB所在直线方程为$y=x-\frac{p}{2}$,可设A(x1,y1),B(x2,y2),直线AB的方程和抛物线方程联立消去x可得到关于y的一元二次方程,由韦达定理即可求出弦AB的中点坐标为$(p,\frac{3p}{2})$,而弦AB的垂直平分线方程可写出为y-2=-x,弦中点坐标带入该方程便可求出p的值.
解答 解:$F(\frac{p}{2},0)$,过焦点F且倾斜角为$\frac{π}{4}$的直线方程为:$y=x-\frac{p}{2}$,设A(x1,y1),B(x2,y2);
由$\left\{\begin{array}{l}{x=y+\frac{p}{2}}\\{{y}^{2}=2px}\end{array}\right.$得,y2-2py-p2=0;
∴y1+y2=2p,x1+x2=3p;
∴弦AB的中点坐标为$(\frac{3p}{2},p)$;
弦AB的垂直平分线方程为y-2=-x,弦AB的中点在该直线上;
∴$p-2=-\frac{3p}{2}$;
解得$p=\frac{4}{5}$.
故选:C.
点评 考查抛物线的标准方程,抛物线的焦点,以及根据直线的倾斜角求斜率,直线的点斜式方程,韦达定理.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目
12.在复平面内,复数(1-2i)2对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
13.下列函数中,既是偶函数又在(0,+∞)上单调递增的是( )
| A. | y=ln|x| | B. | y=$\sqrt{{x}^{2}-1}$ | C. | y=sinx | D. | y=cosx |
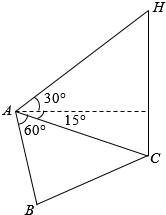 为了应对日益严重的气候问题,某气象仪器科研单位研究出一种新的弹射型气象仪器,这种仪器可以弹射到空中进行气象观测.如图所示,假设这种仪器在C地进行弹射实验,在A,B两地进行观察弹射效果.已知A、B两地相距100米,∠BAC=60°在A地听到弹射声音的时间比B地晚$\frac{2}{17}$秒(已知声音在该地的传播速度为340米/秒),在A地测得该仪器在C处时的俯角为15°,A地测得该仪器至最高点H处的仰角为30°.
为了应对日益严重的气候问题,某气象仪器科研单位研究出一种新的弹射型气象仪器,这种仪器可以弹射到空中进行气象观测.如图所示,假设这种仪器在C地进行弹射实验,在A,B两地进行观察弹射效果.已知A、B两地相距100米,∠BAC=60°在A地听到弹射声音的时间比B地晚$\frac{2}{17}$秒(已知声音在该地的传播速度为340米/秒),在A地测得该仪器在C处时的俯角为15°,A地测得该仪器至最高点H处的仰角为30°.