题目内容
12.在复平面内,复数(1-2i)2对应的点位于( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 利用复数代数形式的乘法运算化简,求出复数所对应点的坐标得答案.
解答 解:∵(1-2i)2 =12-4i+(2i)2=-3-4i,
∴复数(1-2i)2对应的点的坐标为(-3,-4),位于第三象限.
故选:C.
点评 本题考查复数代数形式的乘除运算,考查了复数的代数表示法及其几何意义,是基础题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
2.椭圆的两个焦点和短轴的两个端点,恰好是含60°角的菱形的四个顶点,则椭圆的离心率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$或$\frac{\sqrt{3}}{2}$ | D. | $\frac{1}{2}$或$\frac{\sqrt{3}}{3}$ |
17.已知f(x)是定义在R上的偶函数,且f(2)=8,则f(-2)的值为( )
| A. | -16 | B. | 16 | C. | -8 | D. | 8 |
2.过抛物线y2=2px(p>0)的焦点F,且倾斜角为$\frac{π}{4}$的直线与抛物线交于A,B两点,若弦AB的垂直平分线经过点(0,2),则p等于( )
| A. | $\frac{2}{5}$ | B. | $\frac{2}{3}$ | C. | $\frac{4}{5}$ | D. | $\frac{4}{3}$ |
 如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为梯形,AB∥DC,∠ABC=∠CAD=90°,且PA=AB=BC=1,E是棱PB上的点,且PE=2EB.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为梯形,AB∥DC,∠ABC=∠CAD=90°,且PA=AB=BC=1,E是棱PB上的点,且PE=2EB.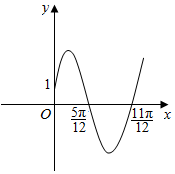 函数f(x)=Asin(ωx+φ),A>0,ω>0,$0<φ<\frac{π}{2}$的图象如右图所示,则f(x)=2sin(2x+$\frac{π}{6}$).
函数f(x)=Asin(ωx+φ),A>0,ω>0,$0<φ<\frac{π}{2}$的图象如右图所示,则f(x)=2sin(2x+$\frac{π}{6}$).