题目内容
12．已知α+β=$\frac{π}{12}$，求$\frac{1-tanα-tanβ-tanα•tanβ}{1+tanα+tanβ-tanα•tanβ}$．分析 由α+β=$\frac{π}{12}$，结合两角和的正切可得1-tanαtanβ=$（2-\sqrt{3}）（tanα+tanβ）$，代入$\frac{1-tanα-tanβ-tanα•tanβ}{1+tanα+tanβ-tanα•tanβ}$后整理得答案．
解答 解：由α+β=$\frac{π}{12}$，得
$tan（α+β）=tan（\frac{π}{3}-\frac{π}{4}）=\frac{tan\frac{π}{3}-tan\frac{π}{4}}{1+tan\frac{π}{3}tan\frac{π}{4}}$=$\frac{\sqrt{3}-1}{\sqrt{3}+1}$，
即$\frac{tanα+tanβ}{1-tanα•tanβ}=\frac{\sqrt{3}-1}{\sqrt{3}+1}=2-\sqrt{3}$，
∴1-tanαtanβ=$（2-\sqrt{3}）（tanα+tanβ）$，
∴$\frac{1-tanα-tanβ-tanα•tanβ}{1+tanα+tanβ-tanα•tanβ}$=$\frac{（2-\sqrt{3}）（tanα+tanβ）-（tanα+tanβ）}{（2-\sqrt{3}）（tanα+tanβ）+（tanα+tanβ）}$
=$\frac{1-\sqrt{3}}{3+\sqrt{3}}=\frac{（1-\sqrt{3}）（3-\sqrt{3}）}{（3+\sqrt{3}）（3-\sqrt{3}）}=\frac{6-4\sqrt{3}}{6}=\frac{3-2\sqrt{3}}{3}$．
点评 本题考查两角和与差的正切函数，考查了计算能力，是中档题．
练习册系列答案
金钥匙试卷系列答案
相关题目
2．过抛物线y2=2px（p＞0）的焦点F，且倾斜角为$\frac{π}{4}$的直线与抛物线交于A，B两点，若弦AB的垂直平分线经过点（0，2），则p等于（ ）
| A． | $\frac{2}{5}$ | B． | $\frac{2}{3}$ | C． | $\frac{4}{5}$ | D． | $\frac{4}{3}$ |
4．设函数f（x）=2k+$\sqrt{x+4}$，若曲线y=cosx上（存在点（x0，y0），使f（f（y0））=y0，则k的取值范围是（ ）
| A． | [--4，$\frac{\sqrt{3}+1}{2}$] | B． | [-$\frac{\sqrt{3}+1}{2}$，$\frac{1-\sqrt{5}}{2}$] | C． | [-$\frac{\sqrt{3}+1}{2}$，$\frac{1+\sqrt{5}}{2}$] | D． | [-4，$\frac{1+\sqrt{5}}{2}$] |
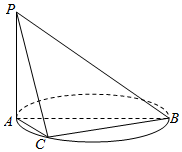如图，AB时圆O的直径，PA垂直圆所在的平面，C是圆上异于A、B的动点，PA=AB，∠ABC大小为θ，点D、E分别在棱PB，PC上．