题目内容
10.经过定点(1,3)作直线l与抛物线y=x2相交于A、B两点.求证:抛物线在A,B两点的切线交点M在一定直线上.分析 设出A,B,则可表示AB的方程,把点(1,3)代入,同时对曲线C的方程求导,判断出A,B处的切线方程,最后联立方程求得结论.
解答 证明:设A(x1,x12),B(x2,x22),(x1≠x2)
则直线AB的方程为:y-x12=(x1+x2)(x-x1),
∵点(1,3)在AB上,
∴3-x12=(x1+x2)(1-x1),即x1+x2-x1x2=3①
对y=x2求导得:y′=2x
∴抛物线上A,B处的切线方程为
y-x12=2x1(x-x1)即y=2x1x-x12②
y-x22=2x2(x-x2)即y=2x2x-x22③
联立②③得x1+x2=2x,x1x2=y
代入①得:2x-y-3=0,
故抛物线在A,B两点的切线交点M在一定直线2x-y-3=0上.
点评 本题主要考查了直线与圆锥曲线的综合问题.考查了学生对问题的综合分析和基本的运算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.过抛物线y2=2px(p>0)的焦点F,且倾斜角为$\frac{π}{4}$的直线与抛物线交于A,B两点,若弦AB的垂直平分线经过点(0,2),则p等于( )
| A. | $\frac{2}{5}$ | B. | $\frac{2}{3}$ | C. | $\frac{4}{5}$ | D. | $\frac{4}{3}$ |
 如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为梯形,AB∥DC,∠ABC=∠CAD=90°,且PA=AB=BC=1,E是棱PB上的点,且PE=2EB.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为梯形,AB∥DC,∠ABC=∠CAD=90°,且PA=AB=BC=1,E是棱PB上的点,且PE=2EB.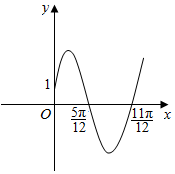 函数f(x)=Asin(ωx+φ),A>0,ω>0,$0<φ<\frac{π}{2}$的图象如右图所示,则f(x)=2sin(2x+$\frac{π}{6}$).
函数f(x)=Asin(ωx+φ),A>0,ω>0,$0<φ<\frac{π}{2}$的图象如右图所示,则f(x)=2sin(2x+$\frac{π}{6}$).