题目内容
11.设数列{an}满足a1=2,an+1=2an-n+1,n∈N*.(1)求数列{an}的通项公式;
(2)若数列{bn}的通项bn=$\frac{1}{n({a}_{n}-{2}^{n-1}+2)}$,求数列{bn}的前n项和Sn.
分析 (1)由数列{an}满足a1=2,an+1=2an-n+1,n∈N*.变形an+1-(n+1)=2(an-n),再利用等比数列的通项公式即可得出.
(2)bn=$\frac{1}{n({a}_{n}-{2}^{n-1}+2)}$=$\frac{1}{n(n+2)}$=$\frac{1}{2}(\frac{1}{n}-\frac{1}{n+2})$,利用“裂项求和”即可得出.
解答 解:(1)∵数列{an}满足a1=2,an+1=2an-n+1,n∈N*.
∴an+1-(n+1)=2(an-n),
∴数列{an-n}是等比数列,首项为1,公比为2,
∴an-n=2n-1,可得∴an=n+2n-1.
(2)bn=$\frac{1}{n({a}_{n}-{2}^{n-1}+2)}$=$\frac{1}{n(n+2)}$=$\frac{1}{2}(\frac{1}{n}-\frac{1}{n+2})$,
∴数列{bn}的前n项和Sn=$\frac{1}{2}[(1-\frac{1}{3})$+$(\frac{1}{2}-\frac{1}{4})$+$(\frac{1}{3}-\frac{1}{5})$+…+$(\frac{1}{n-1}-\frac{1}{n+1})$+$(\frac{1}{n}-\frac{1}{n+2})]$
=$\frac{1}{2}(1+\frac{1}{2}-\frac{1}{n+1}-\frac{1}{n+2})$
=$\frac{3}{4}$-$\frac{2n+3}{2(n+1)(n+2)}$.
点评 本题考查了等比数列的通项公式、递推关系、“裂项求和”方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
2.过抛物线y2=2px(p>0)的焦点F,且倾斜角为$\frac{π}{4}$的直线与抛物线交于A,B两点,若弦AB的垂直平分线经过点(0,2),则p等于( )
| A. | $\frac{2}{5}$ | B. | $\frac{2}{3}$ | C. | $\frac{4}{5}$ | D. | $\frac{4}{3}$ |
16.已知直线:y=kx-k+1与曲线C:x2+2y2=m有公共点,则m的取值范围是( )
| A. | m≥3 | B. | m≤3 | C. | m>3 | D. | m<3 |
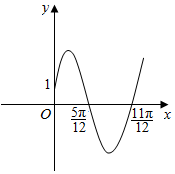 函数f(x)=Asin(ωx+φ),A>0,ω>0,$0<φ<\frac{π}{2}$的图象如右图所示,则f(x)=2sin(2x+$\frac{π}{6}$).
函数f(x)=Asin(ωx+φ),A>0,ω>0,$0<φ<\frac{π}{2}$的图象如右图所示,则f(x)=2sin(2x+$\frac{π}{6}$).