题目内容
设i是虚数单位，复数
+
i是纯虚数，则实数a=（ ）
| 2a+1 |
| 5 |
| a+2 |
| 5 |
| A、-2 | ||
B、
| ||
C、-
| ||
| D、2 |
考点：复数的基本概念
专题：数系的扩充和复数
分析：根据纯虚数的定义，列出方程组，求出实数a的值．
解答：
解：∵复数
+
i是纯虚数，
∴
，
解得a=-
．
故选：C．
| 2a+1 |
| 5 |
| a+2 |
| 5 |
∴
|
解得a=-
| 1 |
| 2 |
故选：C．
点评：本题考查了复数的概念应用问题，解题时应熟练地掌握复数的有关概念，是基础题．
练习册系列答案
相关题目
某三棱锥的三视图如图所示，则该几何体的体积为（ ）
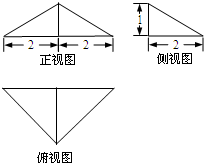
A、
| ||
B、
| ||
C、
| ||
| D、4 |
设函数f（x）=（
x-
）n，其中n=3
cosxdx，则f（x）的展开式中x2的系数为（ ）
| 1 |
| 2 |
| 2 |
| ∫ |
-
|
| A、15 | B、-15 |
| C、60 | D、-60 |
已知下列四个命题：
①底面积和高均相等的柱体体积是锥体体积的3倍：
②正方体的截面是一个n边形，则n的最大值是6；
③在棱长为1的正方体ABCD-AB1C1D1中，三棱锥A1-ABC的体积是
；
④4条棱均为
的四面体的体积是
；
其中真命题的序号是（ ）
①底面积和高均相等的柱体体积是锥体体积的3倍：
②正方体的截面是一个n边形，则n的最大值是6；
③在棱长为1的正方体ABCD-AB1C1D1中，三棱锥A1-ABC的体积是
| 1 |
| 4 |
④4条棱均为
| 2 |
| 1 |
| 3 |
其中真命题的序号是（ ）
| A、①②③ | B、①②④ |
| C、①③④ | D、②③④ |
设i为虚数单位，复数
在复平面上对应的点在（ ）
| 2+i |
| i2 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |