题目内容
已知函数f(x)=log22x-log2x2
(1)求方程f(x)-3=0的解;
(2)当x∈[
,4]时,求函数f(x)的最值,并求f(x)取最值时对应的x的值.
(1)求方程f(x)-3=0的解;
(2)当x∈[
| 1 |
| 2 |
考点:函数的零点,函数的最值及其几何意义
专题:计算题,函数的性质及应用
分析:(1)由题意可得log22x-2log2x-3=0,从而求解方程的根;
(2)利用换元法求函数的最值.
(2)利用换元法求函数的最值.
解答:
解:(1)∵f(x)-3=0,
∴log22x-2log2x-3=0,
∴(log2x-3)(log2x+1)=0,
∴log2x=3或log2x=-1,
∴x=8或
.
(2)设t=log2x,∵x∈[
,4],∴t∈[-1,2],
f(x)=t2-2t=(t-1)2-1,
当t=1,即x=2时,f(x)min=-1,
当t=-1,即x=
时,f(x)max=3.
∴log22x-2log2x-3=0,
∴(log2x-3)(log2x+1)=0,
∴log2x=3或log2x=-1,
∴x=8或
| 1 |
| 2 |
(2)设t=log2x,∵x∈[
| 1 |
| 2 |
f(x)=t2-2t=(t-1)2-1,
当t=1,即x=2时,f(x)min=-1,
当t=-1,即x=
| 1 |
| 2 |
点评:本题考查了函数与方程的关系,同时考查了换元法求函数的最值,属于基础题.

练习册系列答案
相关题目
若函数f(x)=loga(x-1)(a>0,a≠1)的图象恒过定点,则定点的坐标为( )
| A、(1,0) |
| B、(2,0) |
| C、(1,1) |
| D、(2,1) |
“f(x)是奇函数”是“f(0)=0”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
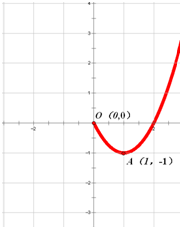 已知f(x)是定义在R上的奇函数,如图为函数f(x)的部分图象.
已知f(x)是定义在R上的奇函数,如图为函数f(x)的部分图象.