题目内容
如图,正方体ABCD-A1B1C1D1中,EF与异面直线AC、A1D都垂直相交.求证:EF∥BD1.
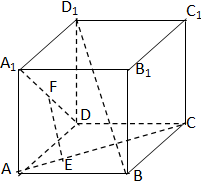

考点:空间中直线与直线之间的位置关系
专题:空间位置关系与距离
分析:连接AB1,B1C,BD,由线面垂直得DD1⊥AC,由BD⊥AC,得AC⊥BD1,同理可证BD1⊥B1C,从而BD1⊥平面AB1C,再由EF⊥平面AB1C,能推导出EF∥BD1.
解答:
证明:如图所示,连接AB1,B1C,BD,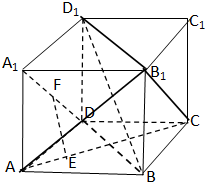
因为DD1⊥平面ABCD,AC?平面ABCD,
所以DD1⊥AC,
又因为BD⊥AC,DD1∩BD=D,
所以AC⊥平面BDD1B1,
所以AC⊥BD1,
同理可证BD1⊥B1C,
又AC∩B1C=C,
所以BD1⊥平面AB1C.…(8分).
因为EF⊥A1D,又A1D∥B1C,
所以EF⊥B1C,
因为EF⊥AC,AC∩B1C=C
所以EF⊥平面AB1C,
所以EF∥BD1.…(12分)

因为DD1⊥平面ABCD,AC?平面ABCD,
所以DD1⊥AC,
又因为BD⊥AC,DD1∩BD=D,
所以AC⊥平面BDD1B1,
所以AC⊥BD1,
同理可证BD1⊥B1C,
又AC∩B1C=C,
所以BD1⊥平面AB1C.…(8分).
因为EF⊥A1D,又A1D∥B1C,
所以EF⊥B1C,
因为EF⊥AC,AC∩B1C=C
所以EF⊥平面AB1C,
所以EF∥BD1.…(12分)
点评:本题考查两直线平行的证明,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
已知f(x)的图象如图所示,则下列数值按从小到大的排列顺序正确的是( )
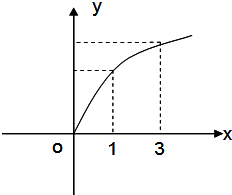

A、f′(1),f′(3),f(0),
| ||
B、f(0),f′(3),
| ||
C、
| ||
D、f(0),
|
下列函数f(x)中,满足“对定义域内的任意一个x都有f(-x)+f(x)=0,且在区间(0,+∞)上恒有
f′(x)>0”的是( )
f′(x)>0”的是( )
A、f(x)=
| ||
| B、f(x)=x2 | ||
| C、f(x)=x3 | ||
| D、f(x)=ex |
不等式|4-3x|-5≤0的解集是( )
A、{x|-
| ||
B、{x|x≤-
| ||
C、{x|
| ||
D、{x|-
|
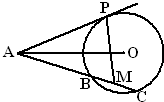 如图,已知AP是⊙O的切线,P为切点,AC是⊙O的割线,且与⊙O交于B、C两点,圆心O在∠PAC的内部,点M是BC的中点,
如图,已知AP是⊙O的切线,P为切点,AC是⊙O的割线,且与⊙O交于B、C两点,圆心O在∠PAC的内部,点M是BC的中点,