题目内容
一束光线从点A(-2,2)出发.经X轴反射到⊙C:(x-2)2+(y-3)2=1上的路径最短长度是 .
考点:与直线关于点、直线对称的直线方程
专题:直线与圆
分析:求出点A关于x轴的对称点A′,则要求的最短路径的长为A′C-r(圆的半径),计算求得结果.
解答:
 解:由题意可得圆心C(2,3),半径为r=1,点A关于x轴的对称点A′(-2,-2),
解:由题意可得圆心C(2,3),半径为r=1,点A关于x轴的对称点A′(-2,-2),
求得A′C=
,则要求的最短路径的长为A′C-r=
-1,
故答案为:
-1.
 解:由题意可得圆心C(2,3),半径为r=1,点A关于x轴的对称点A′(-2,-2),
解:由题意可得圆心C(2,3),半径为r=1,点A关于x轴的对称点A′(-2,-2),求得A′C=
| 41 |
| 41 |
故答案为:
| 41 |
点评:本题主要考查反射定理的应用,求一个点关于直线的对称点的方法,体现了转化、数形结合的数学思想,属于基础题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
当a>1时,在同一坐标系中,函数y=a-x与y=logax的图象为( )
A、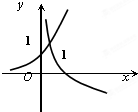 |
B、 |
C、 |
D、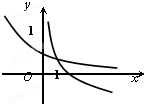 |
已知f(x)的图象如图所示,则下列数值按从小到大的排列顺序正确的是( )
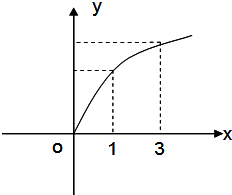

A、f′(1),f′(3),f(0),
| ||
B、f(0),f′(3),
| ||
C、
| ||
D、f(0),
|
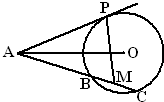 如图,已知AP是⊙O的切线,P为切点,AC是⊙O的割线,且与⊙O交于B、C两点,圆心O在∠PAC的内部,点M是BC的中点,
如图,已知AP是⊙O的切线,P为切点,AC是⊙O的割线,且与⊙O交于B、C两点,圆心O在∠PAC的内部,点M是BC的中点,