题目内容
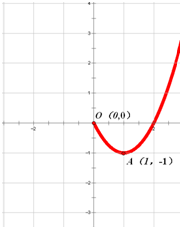 已知f(x)是定义在R上的奇函数,如图为函数f(x)的部分图象.
已知f(x)是定义在R上的奇函数,如图为函数f(x)的部分图象.(1)请你补全它的图象;
(2)求f(x)在R上的表达式;
(3)写出f(x)在R上的单调区间(不必证明).
考点:函数奇偶性的性质
专题:计算题,作图题,函数的性质及应用
分析:(1)由函数的对称性补全它的图象;
(2)设f(x))=a(x-0)(x-2),从而求出函数解析式,由奇函数解对称区间上的解析式;
(3)由图象写出函数的单调区间.
(2)设f(x))=a(x-0)(x-2),从而求出函数解析式,由奇函数解对称区间上的解析式;
(3)由图象写出函数的单调区间.
解答:
解:(1)

(2)当x≥0时,设f(x)=a(x-0)(x-2),
把A点(1,-1)代入,解得a=1,
∴f(x)=x2-2x,(x≥0),
当x<0时,
∵f(x)为R上的奇函数,
∴f(x)=-f(-x)=-[(-x)2-2(-x)]=-x2-2x,
∴f(x)=
;
(3)由图知,f(x)在(-∞,-1]和[1,+∞)上单调递增,f (x)在(-1,1)上单调递减.

(2)当x≥0时,设f(x)=a(x-0)(x-2),
把A点(1,-1)代入,解得a=1,
∴f(x)=x2-2x,(x≥0),
当x<0时,
∵f(x)为R上的奇函数,
∴f(x)=-f(-x)=-[(-x)2-2(-x)]=-x2-2x,
∴f(x)=
|
(3)由图知,f(x)在(-∞,-1]和[1,+∞)上单调递增,f (x)在(-1,1)上单调递减.
点评:本题考查了函数的解析式的求法,图象的作法及单调区间的写法,属于基础题.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
已知集合A到B的映射f:x→y=
,则集合A中元素3在B中所对应的元素是( )
| 12 |
| x+1 |
| A、1 | B、2 | C、3 | D、4 |
已知等差数列{an}的公差d≠0,a1≠d,若前20项的和S20=10M,则M等于( )
| A、a1+2a10 |
| B、a6+a15 |
| C、a20+d |
| D、2a10+2d |
下列关系中正确的是( )
A、log76<ln
| ||
B、log3π<ln
| ||
C、ln
| ||
D、ln
|
 三棱柱ABC-A1B1C1中,侧棱与底面垂直,∠ABC=90°,AB=BC=BB1=2,M,N分别是AB,A1C的中点.
三棱柱ABC-A1B1C1中,侧棱与底面垂直,∠ABC=90°,AB=BC=BB1=2,M,N分别是AB,A1C的中点.