题目内容
19.已知双曲线的渐近线方程为y=±$\frac{3}{4}$x,则此双曲线的( )| A. | 焦距为10 | B. | 实轴长与虚轴长分别为8与6 | ||
| C. | 离心率e只能是$\frac{5}{4}$或$\frac{5}{3}$ | D. | 离心率e不可能是$\frac{5}{4}$或$\frac{5}{3}$ |
分析 利用双曲线的渐近线方程,推出ab关系,然后求解离心率即可.
解答 解:双曲线的渐近线方程为y=±$\frac{3}{4}$x,
当双曲线的焦点坐标在x轴时,$\frac{b}{a}=\frac{3}{4}$,
可得$\frac{{c}^{2}-{a}^{2}}{{a}^{2}}=\frac{9}{16}$,解得e=$\frac{5}{4}$.
当双曲线的焦点坐标在y轴时,$\frac{a}{b}=\frac{3}{4}$,
可得16a2=9c2-9a2,解得e=$\frac{5}{3}$.
故选:C.
点评 本题考查双曲线的简单性质的应用,考查计算能力.

练习册系列答案
相关题目
9.某市在一次降雨过程中,降雨量y(mm)与时间t(min)的函数关系可近似地表示为y=f(t)=$\sqrt{t}$,则在时刻t=40min的降雨强度为( )
| A. | 40mm | B. | 40$\sqrt{10}$mm | C. | $\frac{1}{40}$mm/min | D. | $\frac{\sqrt{10}}{40}$mm/min |
10.在空间直角坐标系O-xyz中,若O(0,0,0),A(0,2,0),B(2,0,0),C(2,2,2$\sqrt{3}$),则二面角C-OA-B的大小为( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
4.设集合M={x|2x+1>1},N={x|lnx≤1},则M∩N等于( )
| A. | (-∞,e] | B. | (-1,1] | C. | (0,1) | D. | (0,e] |
11. 秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入x的值为2,则输出v的值为( )
秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入x的值为2,则输出v的值为( )
 秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入x的值为2,则输出v的值为( )
秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入x的值为2,则输出v的值为( )| A. | 210-1 | B. | 210 | C. | 310-1 | D. | 310 |
8.一个圆锥的底面圆半径为3,高为4,则这个圆锥的侧面积为( )
| A. | $\frac{15π}{2}$ | B. | 24π | C. | 15π | D. | 20π |
9.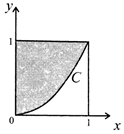 在如图所示的正方形中随机投掷10000个点,则落入阴影部分(曲线C的方程为x2-y=0)的点的个数的估计值为( )
在如图所示的正方形中随机投掷10000个点,则落入阴影部分(曲线C的方程为x2-y=0)的点的个数的估计值为( )
 在如图所示的正方形中随机投掷10000个点,则落入阴影部分(曲线C的方程为x2-y=0)的点的个数的估计值为( )
在如图所示的正方形中随机投掷10000个点,则落入阴影部分(曲线C的方程为x2-y=0)的点的个数的估计值为( )| A. | 5000 | B. | 6667 | C. | 7500 | D. | 7854 |
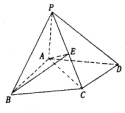 在四棱锥P-ABCD中,△ABC为正三角形,AB⊥AD,AC⊥CD,PA⊥平面ABCD,PC与平面ABCD所成角为45°
在四棱锥P-ABCD中,△ABC为正三角形,AB⊥AD,AC⊥CD,PA⊥平面ABCD,PC与平面ABCD所成角为45°