题目内容
10.在空间直角坐标系O-xyz中,若O(0,0,0),A(0,2,0),B(2,0,0),C(2,2,2$\sqrt{3}$),则二面角C-OA-B的大小为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
分析 设C在平面xoy上的射影为D,则可得OA⊥平面ACD,故∠CAD为所求二面角的平面角.
解答  解:设C在平面xoy上的射影为D(2,2,0),连接AD,CD,BD,
解:设C在平面xoy上的射影为D(2,2,0),连接AD,CD,BD,
则CD=2$\sqrt{3}$,AD=OA=2,四边形OBDA是正方形,
∴OA⊥平面ACD,
∴∠CAD为二面角C-OA-B的平面角,
∵tan∠CAD=$\frac{CD}{AD}$=$\frac{2\sqrt{3}}{2}$=$\sqrt{3}$,
∴∠CAD=60°.
故选C.
点评 本题考查了二面角的作法与计算,属于中档题.

练习册系列答案
相关题目
9.已知0<a<b,且a+b=1,则下列不等式中正确的是( )
| A. | log2a>0 | B. | 2a-b<$\frac{1}{2}$ | C. | log2a+log2b<-2 | D. | 2($\frac{a}{b}$+$\frac{b}{a}$)<$\frac{1}{2}$ |
1.已知命题p:?x∈R,2x2+2x+$\frac{1}{2}$<0,命题q:?x0∈R,sinx0-cosx0=$\sqrt{2}$,则下列判断中正确的是( )
| A. | p是真命题 | B. | q是假命题 | C. | ¬p是假命题 | D. | ¬q是假命题 |
15.圆柱被一个平面截去一部分后与一个四棱锥组成的几何体的三视图如图所示,则该几何体的体积为( )
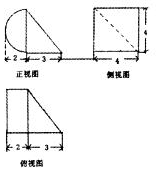

| A. | 4π+8 | B. | 8π+16 | C. | 16π+16 | D. | 16π+48 |
19.已知双曲线的渐近线方程为y=±$\frac{3}{4}$x,则此双曲线的( )
| A. | 焦距为10 | B. | 实轴长与虚轴长分别为8与6 | ||
| C. | 离心率e只能是$\frac{5}{4}$或$\frac{5}{3}$ | D. | 离心率e不可能是$\frac{5}{4}$或$\frac{5}{3}$ |
20.某几何体的三视图如图所示,则该几何体的体积为( )


| A. | 5 | B. | $\frac{16}{3}$ | C. | 7 | D. | $\frac{17}{3}$ |